Lineare Abhängigkeit Vektor

Question

Aufgabe:

Gegeben sind die Vektoren a ( 3/-3/7) und b (9/-1/21).
Gesucht ist ein Vektor c , so dass a , b und c linear abhängig sind.

Der Nullvektor ist nicht zulässig.

Bitte um die Lösung + Lösungsweg :) Danke.

Comments

Vom Duplikat:

Titel: Vektoren linear abhängig

Stichworte: vektoren

Hallo zusammen,

ich komme bei der Aufgabe nicht weiter, wäre froh wenn mir jemand helfen könnte mit einer Erklärung.

Vielen Dank!

Text erkannt:

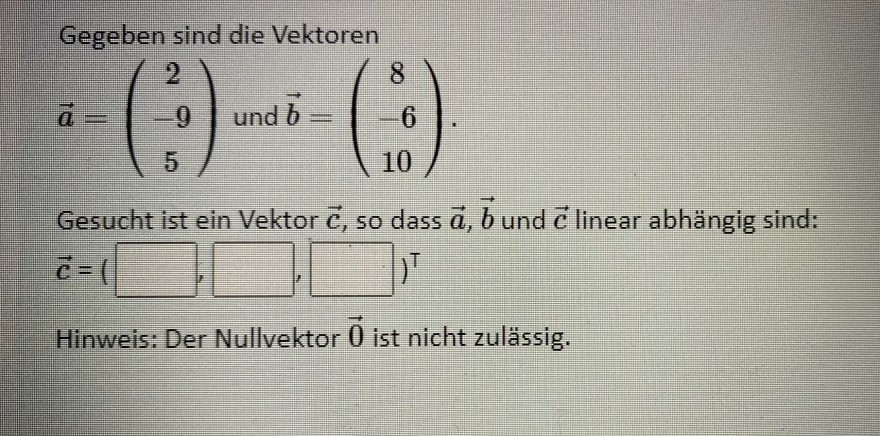
Gegeben sind die Vektoren
\( \vec{a}=\left(\begin{array}{c} 2 \\ -9 \\ 5 \end{array}\right) \text { und } \vec{b}=\left(\begin{array}{c} 8 \\ -6 \\ 10 \end{array}\right) \)
Gesucht ist ein Vektor \( \vec{c} \), so dass \( \vec{a}, \vec{b} \) und \( \vec{c} \) linear abhängig sind: \( \vec{c}=0 \)
Hinweis: Der Nullvektor \( \overrightarrow{0} \) ist nicht zulässig.

---

vgl. https://www.mathelounge.de/889105

---

Oh hab ich nicht gesehen, danke dir

Answer 1

Aloha :)

Addiere die beiden Vektoren doch einfach:$$\vec c=\vec a+\vec b=\begin{pmatrix}3\\-3\\7\end{pmatrix}+\begin{pmatrix}9\\-1\\21\end{pmatrix}=\begin{pmatrix}12\\-4\\28\end{pmatrix}$$

Comments

Das wars? Und die sind dann dadurch linear Abhängig?

Danke dir.

---

Ja, denn du kannst jeden Vektor durch die beiden anderen ausdrücken:$$\vec c=\vec a+\vec b$$$$\vec a=\vec c-\vec b$$$$\vec b=\vec c-\vec a$$

Du kannst dir merken, dass Vektoren linear abhängig sind, wenn man sie (mit Dehnung oder Kürzung durch Vorfaktoren) zu einem geschlossenen Vektorzug addieren kann:$$\vec c+(-1)\cdot\vec a+(-1)\cdot\vec b=\vec 0$$

Answer 2

Hallo,

denk dir zwei beliebige Zahlen r und s, allerdings nicht gleichzeitig r=0 und s=0.

Berechne

\(\vec{c}=r\cdot \vec{a}+s\cdot\vec{b}\)

Das ist eine Linearkombination von \( \vec{a} \) und \( \vec{b} \).

:-)