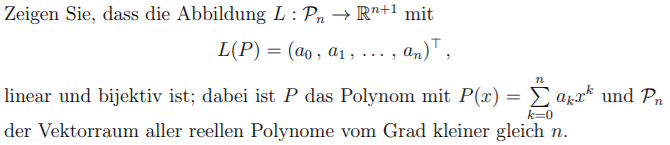
Text erkannt:
Zeigen Sie, dass die Abbildung \( L: \mathcal{P}_{n} \rightarrow \mathbb{R}^{n+1} \) mit
\( L(P)=\left(a_{0}, a_{1}, \ldots, a_{n}\right)^{\top} \)
linear und bijektiv ist; dabei ist \( P \) das Polynom mit \( P(x)=\sum \limits_{k=0}^{n} a_{k} x^{k} \) und \( \mathcal{P}_{n} \) der Vektorraum aller reellen Polynome vom Grad kleiner gleich \( n \).
Aufgabe:
Zeigen Sie, dass die Abbildung L : Pn → Rn+1
mit L(P) = (a0 , a1 , . . . , an) linear und bijektiv ist.
Pn ist der Vektorraum aller reellen Polynome vom Grad kleiner gleich n und P die allgemeine Form eines Polynoms P(x)
Problem/Ansatz:
Die Linearität habe ich soweit. Nun möchte ich die Bijektivität mithilfe der Umkehrabbildung zeigen. Wie mache ich das bei einem allgemeinen Polynom?