3. Tangentenproblem mittels pq-Formel

Question

Aufgabe:

Funktion f(x) = 5x²

Punkt A außerhalb der Funktion A(1|3)

Tangentengleichung mittels der pq-Formel bestimmen (3. Tangentenproblem)

Problem/Ansatz:

Wir hatten das Ganze in der Schule, es war aber sehr unverständlich zu verstehen, vielleicht könnte es ja jemand hier nochmal ausführlicher an dem Beispiel erklären, würde mir sehr helfen.

Im Mathebuch steht darüber leider nichts, auch im Internet findet man kaum zum 3. Tangentenproblem Lösungswege mittels der pq-Formel.

LG

Answer 1

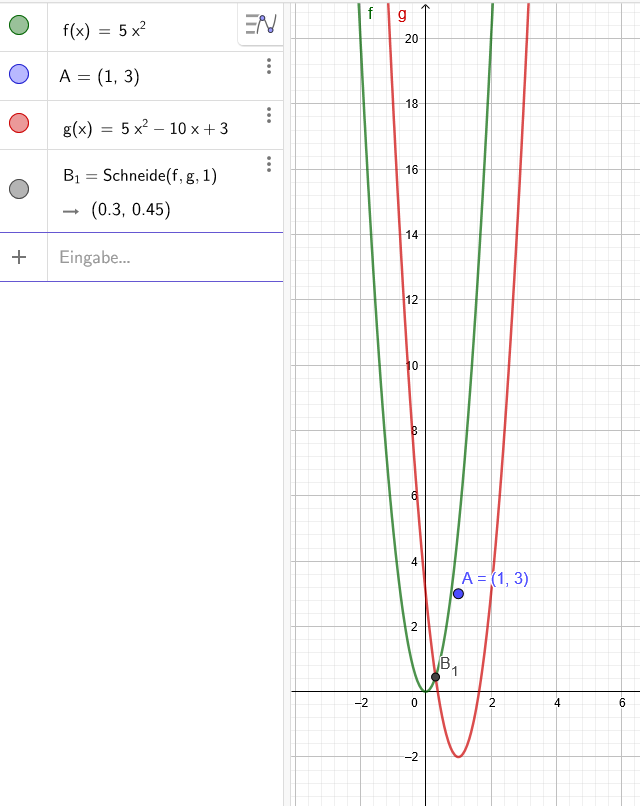
f(x) = 5x²      A(1|3)

f´(x)=10x

\( \frac{y-3}{x-1} \)=10x

y=10x^2-10x+3

10x^2-10x+3=5x^2

5x^2-10x=-3

x^2-2x=-\( \frac{3}{5} \)

(x-1)^2=-\( \frac{3}{5} \)+1=\( \frac{2}{5} \)|\( \sqrt{} \)

1.)x-1=\( \sqrt{0,4} \)

x₁=1+\( \sqrt{0,4} \)       y₁=5*(1+\( \sqrt{0,4} \))^2

2.)x-1=-\( \sqrt{0,4} \)

x₂=1-\( \sqrt{0,4} \)       y₂=5*(1-\( \sqrt{0,4} \))^2

Jetzt hast du die beiden Berührpunkte und kannst die 2 Tangenten berechnen.

Comments

Danke für die gute Antwort!

Kann man dies auch in einzelne Schritte unterteilen? Dies hilft mir persönlich beim verstehen und lernen noch besser

Answer 2

Nenne einen möglichen Berührpunkt der Tangente (u|v).

Dann gilt (1) v=5u²

             (2) \( \frac{3-u}{1-v} \)=10u.

Löse dies System und finde zwei Paare (u|v), die der Bestimmung zweier Tangentengleichungen dienen (zB. Zwei-Punkte-Form).

Answer 3

$$f(x)=5x^2,\quad A(1\vert 3)$$ Seien \(B(b\vert f(b))\) die Koordinaten der jeweiligen Berührpunkte. Die Tangenten genügen dann der Gleichung $$y=f'(b)\cdot\left(x-x_1\right)+y_1$$ für einen Punkt \((x_1\vert y_1)\) auf der jeweiligen Tangente. Eingeben aller genannten Informationen ergibt $$5b^2=10b\cdot\left(b-1\right)+3$$ ergibt eine quadratische Bestimmungsgleichung für die Berührstellen \(b\). Mit dem nach dem Lösen der Gleichung ausrechenbaren \(f'(b)\) lassen sich die Tangentengleichungen nun als $$y=f'(b)\cdot\left(x-1\right)+3$$ angeben.