Wie kann man hier die Integrationsgrenzen bestimmen

Question

Aufgabe:

Kann jemand mir erklären, wie ich diese Aufgabe machen kann ?

Problem/Ansatz:

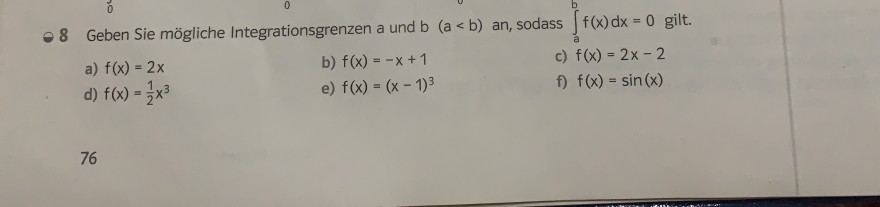
Text erkannt:

08 Geben Sie mögliche Integrationsgrenzen a und $b(a<b)$ an, sodass $\int \limits_{a}^{b} f(x) d x=0$ gilt.
a) $f(x)=2 x$
b) $f(x)=-x+1$
c) $f(x)=2 x-2$
d) $f(x)=\frac{1}{2} x^{3}$
e) $f(x)=(x-1)^{3}$
f) $f(x)=\sin (x)$
76

Answer 1

Zeichne die jeweils zugehörigen Graphen und bedenke, dass Flächen unterhalb der x-Achse negativ in das Integral eingehen. Dann kannst du die Integrationsgrenzen in der Skizze ablesen.

Answer 2

Hallo,

zeichne den Graphen zu a und du siehst, das Integral ist 0 wenn a und b Gegenzahlen sind, hier z.B. -2 und 2

Skizze zu d):

e) Symmetriezentrum bei x = 1

f)

Gruß, Silvia

Comments

Hallo Silvia,

statt Symmetrieachse muss es Symmetriezentrum heißen.

:-)

---

Stimmt, ungerade Funktion, ich korrigiere das. Danke!

Symmetriepunkt geht aber auch, oder?

---

Ich habe es schon geändert.

:-)

Den Begriff Symmetriepunkt kenne ich nicht.

:-)

---

Dann entsprang er wohl meiner Phantasie und ich streiche ihn wieder.