Das Integral soll durch Substituieren gelöst werden:
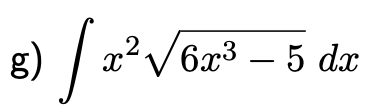
Mein Rechenweg gibt aber ein anderes Ergebnis, als die Musterlösung:
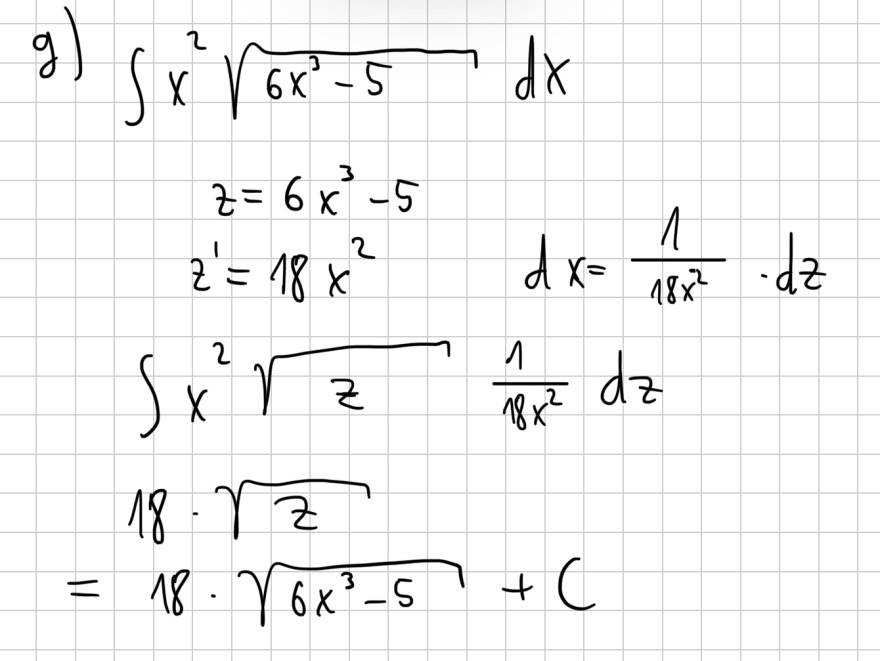
Text erkannt:
g) \( \begin{aligned} & \int x^{2} \sqrt{6 x^{3}-5} d x \\ & z=6 x^{3}-5 \\ & z^{\prime}=18 x^{2} \\ & \int x^{2} \sqrt{z} \frac{1}{18 x^{2}} d z=\frac{1}{18 x^{2}} \cdot d z \\ & 18 \cdot \sqrt{z} \\=& 18 \cdot \sqrt{6 x^{3}-5}+C \end{aligned} \)
Wo liegt der Fehler?
Text erkannt:
g) \( \int x^{2} \sqrt{6 x^{3}-5} d x \)