Integral f(x)dx bestimmen. f(x):=√x.

Question

Sei \( f:[0,1] \rightarrow \mathbb{R}, x \mapsto \sqrt{x} \). Bestimmen Sie \( \int \limits_{0}^{1} f(x) d x \)

Answer 1

Wurzel (x) = x hoch (1/2)

Das solltest Du jetzt leicht integrieren können.

Anschließend die Grenzen einsetzen.

Comments

Kommt dann 1 als Antwort raus?

---

Nein.

Welche Klasse bist Du ? 11 oder 12 ?

Answer 2

Falls du die Stammfunktion von Wurzel x noch nicht benutzen darfst.

Integriere

∫_o¹ y^2 dy = 1/3 y^3 |_o¹ = = 1/3 -0 = 1/3.

Nun bekommst du die gesuchte Fläche, indem du 1-1/3 = 2/3 berechnest. 

Erklärung mit Skizze: Statt die Fläche unter der Kurve y=√x zu berechnen, schaue ich das Koordinatensystem andersrum an. Die Funktionsgleichung ist dann x = y^2 und wenn ich von 0 bis 1 integriere, bekomme ich die Fläche oberhalb der blauen Kurve. Nun habe die gesuchte und die berechnete Fläche zusammen die Fläche des Quadrates (also 1).

Daher  ∫_o¹ √x dx = 1-1/3 = 2/3

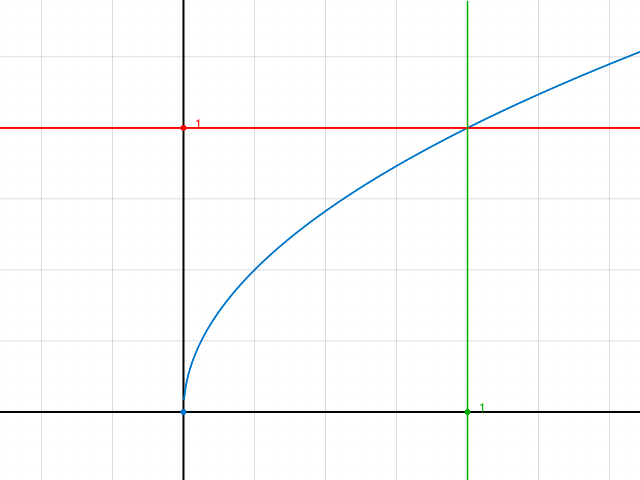
Es ist übrigens Zufall, dass man hier bei beiden Integralen von 0 bis 1 integriert. Man muss dafür sorgen, dass sich die grüne und die rote Linie auf der Kurve treffen.

Anderes Beispiel: x läuft von 0 bis 4 heisst y läuft von 0 bis 2.