Bestimmen sie die Gleichung der Normalen an den Graphen von f im Punkt A

Question

Aufgabe: Bestimmen sie die Gleichung der Normalen an den Graphen von f im Punkt A

c) f(x)=2/x+1/4x+3/2

A:(4|f(4))

d) f(x)=WurzelX-X+2

A(1|f(1))

Hab aufgabenteile a)+b) hinbekommen mir fehlt jetzt aber c+d?

Hilfe?

Comments

f(x)=2/x+1/4x+3/2

f(x)=\( \frac{2}{x} \)+\( \frac{1}{4} \)x+\( \frac{3}{2} \)

oder

f(x)=\( \frac{2}{x} \)+\( \frac{1}{4x} \)+\( \frac{3}{2} \)

---

Hey,danke dir hättest du noch den Lösungswegparat und die Lösung zur anderen?

---

Lautet die Funktion so
f ( x ) = 2/x + (1/4) * x + 3/2

---

Hey,danke dir hättest du noch den Lösungswegparat und die Lösung zur anderen?

Hmm, das beantwortet Moliets' Frage nicht.

---

1/4*X

Ist es

Sorry bin verpeilt

Answer 1

Hallo

c) f'(x) bilden da du f ja im Gegensatz zu uns kennst, dann die Gerade mit der Steigung m=-1/f'(4) durch A aufstellen d) entsprechen mit m=-1/f'(1)

denn -1/f'(x) ist senkrecht bzw normal zur Tangentensteigung in x

Gruß lul

Answer 2

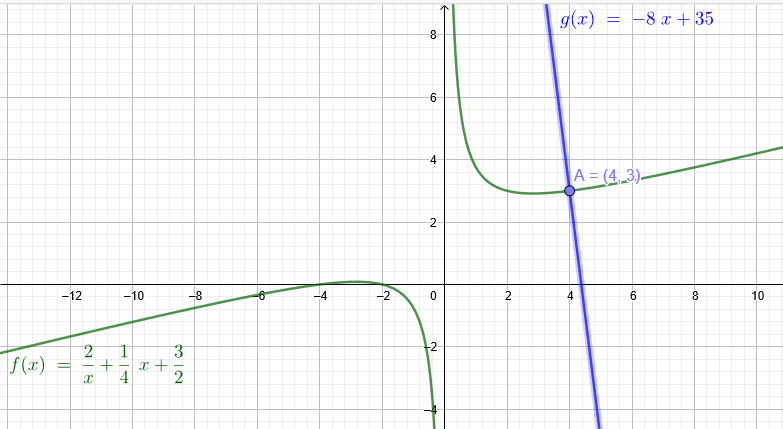
f ( x ) = 2/x + (1/4) * x + 3/2

A:(4|f(4))

f ( 4 ) = \( \frac{2}{4} \) + \( \frac{1}{4} \) * 4+ \( \frac{3}{2} \)=3

f´(x)=-\( \frac{2}{x^2} \)+\( \frac{1}{4} \)

A:(4|f(4))

f´(4)=-\( \frac{2}{4^2} \)+\( \frac{1}{4} \)=\( \frac{1}{8} \)

Normalensteigung : m=-8

Normalengleichung:

\( \frac{y-3}{x-4} \)=-8

y=-8x+35

Comments

Danke dir.

Bist mein Retter für c) schonmal

---

\( A(1 \mid 2) \)
\( f(x)=\sqrt{x}-x+2 \)
\( \begin{array}{l} \frac{d f(x)}{d x}=\frac{1}{2 \sqrt{x}}-1 \\ \frac{d f(1)}{d x}=\frac{1}{2 \sqrt{1}}-1=-\frac{1}{2} \end{array} \)
Normalensteigung \( m=2 \)
\( \begin{array}{l} \frac{y-2}{x-1}=2 \\ y=2 x \end{array} \)

---

Danke dir.

:)

Vielen Dank

---

Hi bei der d) ist der Punkt A (1|f(1))

Answer 3

c)

n(x) = (x- 4)* (-1)/f '(4) +f(4)

d) analog

Answer 4

Gegeben
f ( x )
und
P ( xp | yp )

Steigung Tangente
f ´ ( x) = m
Steigung Normale
m2 = -1 / m

yp = m2 * xp + b
b =

Normalengleichung
n ( x ) = m2 * x + b