Aufgabe:
Sei…
f1 (x) = x^3 -9x
f2 (x) = x(x+ 3)^2
f3 (x) = -x^2(x+3)
a)
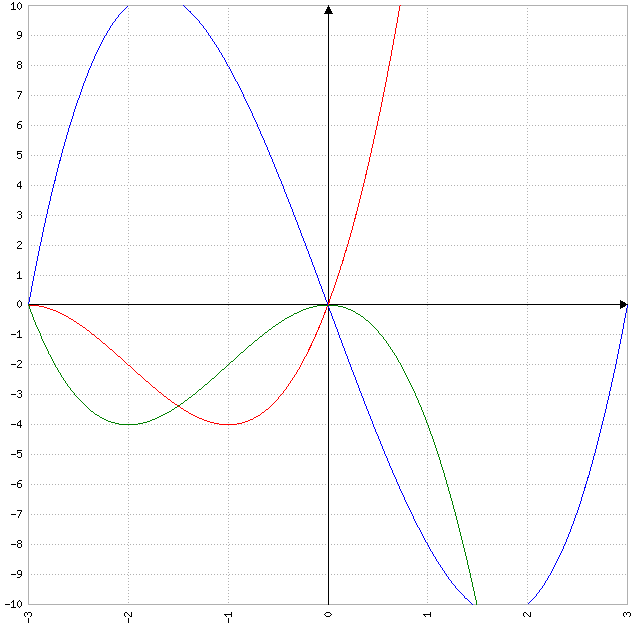
Die Abbildung zeigt die Graphen der
drei Funktionen. Ordnen Sie jeder
Funktion den entsprechenden Graphen
zu. Begründen Sie Ihre Entscheidung.
b)
Sei g(x) = f1(x) + f2(x) + f3(x). Bestimmen Sie die Nullstellen und Extrema von g. Skizzieren Sie den Graphen von g.
c)
Begründen Sie, dass man den Graphen
von g aus den vorgegebenen Graphen
durch eine geeignete Spiegelung erhalten kann.
d)
Welche Beziehung besteht damit zwischen den drei gegebenen Funktionen?
e)
Welche Winkel bilden die Wendetangente an den Graphen von g und die Tangente an den
Graphen von g in der Nullstelle links vom Ursprung miteinander?
Problem/Ansatz:
Ich hab a), b) schon. e) hab ich teilweise, da ich auch nicht mehr weiter kam. Bei c und d weiß ich halt nicht wie ich das jetzt angehen soll. Bitte helfen!