Bestimmen Sie ihren Abstand. und Lage von Geraden

Question

Aufgabe:

Untersuchen Sie die gegenseitige Lage der Geraden g und h. Bestimmen Sie ihren Abstand.

a) g: x = {2|5|5} + t * {1|1|3}; h: x = t * {-1|-1|3}

Problem/Ansatz:

Lage: windschief

Abstand: ungefähr 15,65 LE

Beim Abstand bin ich mir unsicher, ist das richtig?

Answer 1

Hallo,

Abstand: ungefähr 15,65 LE

das ist zu viel. Das sieht man schon an dem Bild hier

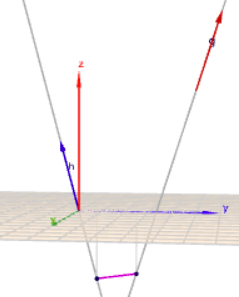
(klick drauf, dann hast Du es in groß)

Mein Abstand \(d\) ist $$d = \frac 32\sqrt{2} \approx 2,12$$Zeige bitte Deine Rechnung, dann kann man den Fehler finden.

Gruß Werner

Comments

Habe es mit der Orthogonalität berechnet:

Habe die Gleichungen:

-11t+7s-22=0

-7t+11s-8=0 raus

---

Die allgemeinen Geradenpunkte, da habe ich

G(2+t/5+t/5+3t) und H(-s/-2/3s)

Vektor GH=(-s-2-t/-s-5-t/3s-5-3t)

---

Alles gut hab meinen Fehler gefunden, aber Danke!

---

Habe die Gleichungen:
-11t+7s-22=0
-7t+11s-8=0 raus

das habe ich auch. Als Lösung habe ich$$t=-\frac{31}{12}, \quad s=-\frac{11}{12}$$

Die allgemeinen Geradenpunkte, da habe ich
G(2+t/5+t/5+3t) und H(-s/-2/3s)

Du meinst wahrscheinlich \(H(-s|\,-s|\, 3s)\)

---

Habe gerade gesehen das ich bei der 3 in der Geradengleichung ein - vergessen habe uns sie somit parallel sind.

Habe sie da eine Tipp wie ich den Abstand dort berechne, weil der Normalenvektor ja 000 wäre

---

Habe sie da eine Tipp wie ich den Abstand dort berechne

wenn die Geraden parallel sind, dann nehme einen beliebigen Punkt auf einer Geraden (hier z.B. \((2|\,5|\,5)\) auf \(g\)) und berechne den Abstand zur anderen - also hier zu \(h\).

hier habe ich \(d=\sqrt{10}\approx 3,16\).