Frauen, Männer und der Intelligenzquotient

Question

In Deutschland liegt der durchschnittliche Intelligenzquotient bei ziemlich genau 100. Er ist ebenfalls ziemlich genau Gauß-verteilt:

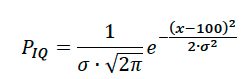
Überraschend ist, dass das für Frauen und Männer unterschiedlich ist: ♀=13,239 ♂=16,178

Etwa 1 ‰ der deutschen Bevölkerung sind höchstintelligent mit ≥145. Zeigen Sie aus dem obigen, dass es ca. achtmal mehr höchstintelligente Männer als Frauen gibt! (Es gibt aber auch unter den extrem minderintelligenten achtmal mehr Männer als Frauen, was sich aus Symmetriegründen genauso zeigen lässt)

(Hinweis: zur Lösung brauchen Sie die Fehlerfunktion, die z. B. in Excel oder vielen Taschenrechnern eine fest programmierte Funktion ist)

Comments

♀=13,239 ♂=16,178

Soll das die Standardabweichung sein, die Varianz, oder (was ich nicht hoffe) der IQ?

---

standardabweichung :-) sorry

---

Dann teile das bitte auch den Leuten im ebenfalls behelligten Nachbarforum mit, dass die nicht auch noch rückfragen müssen.

---

Benutzer hat den Zugang zur Mathelounge bereits schon gelöscht und ist zu "Gast" geworden.

Was ist das für ein Nachbarforum?

---

onli**mathe.de

(Dort hat sich der Name gerade in "anonymous" geändert.)

Answer 1

Wo ist genau das Problem?

(1 - NORMAL((145 - 100)/16.178))/(1 - NORMAL((145 - 100)/13.239)) = 8.000370420

1/2·((1 - NORMAL((145 - 100)/16.178)) + (1 - NORMAL((145 - 100)/13.239))) = 0.001521530201

Demnach sollten 1.5 ‰ hochintelligent sein.

Comments

was ist das für eine Formel?

---

was ist das für eine Formel?

WK für einen hochintelligenten Mann durch WK für eine hochintelligente Frau sollte nach Text ungefähr 8 sein. Also rechnet man das einfach mal aus.

NORMAL() steht hier für die Standardnormalverteilung.

Answer 2

Mit

\( \frac{1}{13.239 \sqrt{2 \pi}} \int \limits_{145}^{\infty} e^{-(t-100)^{2}/ (2 \cdot 13.239^2)} d t \)

kommst Du auf einen Anteil von ca. 0,000338104 höchstintelligenter Frauen und mit

\( \frac{1}{16.178 \sqrt{2 \pi}} \int \limits_{145}^{\infty} e^{-(t-100)^{2}/ (2 \cdot 16.178^2)} d t \)

auf einen Anteil von ca. 0,00270496 höchstintelligenter Männer.

Das ist der in der Aufgabe genannte Faktor von ca. 8.