Welche Vektoren sind gleich, welche sind Vielfache voneinander, aber nicht gleich?

Question

Aufgabe:

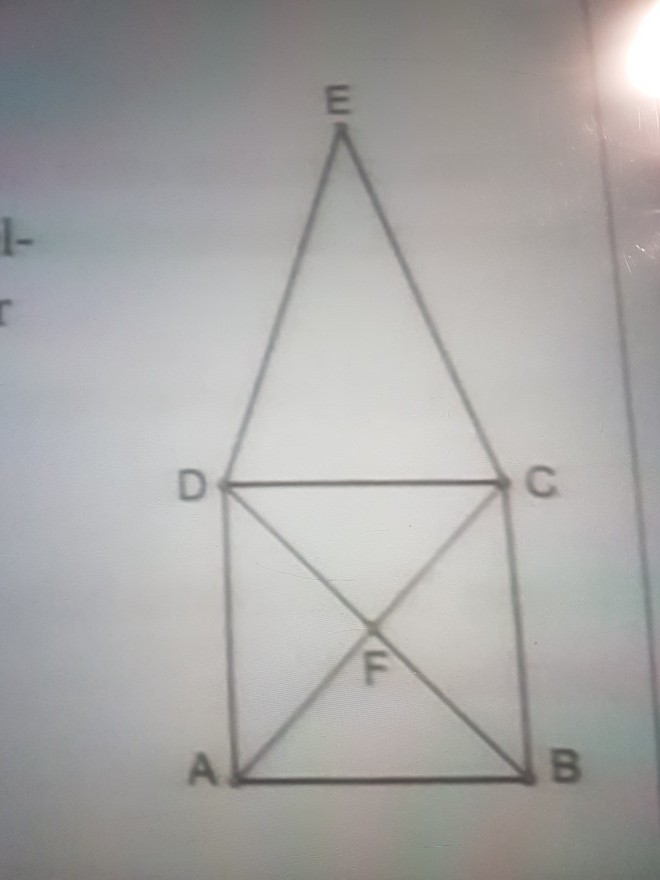welche vektoren sind gleich, welche sind vielfache voneinander, aber nicht gleich?

Lösung:

Gleiche Veltoren:
\( \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{BC}}, \space \overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}} \),
\( \overrightarrow{\mathrm{AF}}=\overrightarrow{\mathrm{FC}}, \space \overrightarrow{\mathrm{DF}}=\overrightarrow{\mathrm{FB}} \)

Vielfache voneinander:
\( \overrightarrow{\mathrm{AC}} \) und \( \overrightarrow{\mathrm{AF}}, \space \overrightarrow{\mathrm{AC}} \) und \( \overrightarrow{\mathrm{FC}} \),
\( \overrightarrow{\mathrm{DB}} \) und \( \overrightarrow{\mathrm{PB}}, \space \overrightarrow{\mathrm{DB}} \) und \( \overrightarrow{\mathrm{DF}} \).

Problem/Ansatz:

Aber was ist mit \( \overrightarrow{\mathrm{DE}}, \space \overrightarrow{\mathrm{CE}} \) usw? Warum ist \( \overrightarrow{\mathrm{AC}}\ \) nur ein Vielfaches? Ist das nicht auch gleich?

Answer 1

DE und CE sind zwar gleich lang, weisen aber nicht in die gleiche Richtung

AC und AF weisen zwar in die gleiche Richtung, sind aber leider nicht gleich lang.

Zwei Vektoren sind gleich, wenn sie in die gleiche Richtung weisen und gleich lang sind.

Comments

DE und CE sind zwar gleich lang, weisen aber nicht in die gleiche Richtung

Woran sehen Sie das? Da ist doch kein Pfeil von einem zum anderen Punkt. Also ich weiß nicht, woran ich das festmachen soll..

---

Da ist doch kein Pfeil von einem zum anderen Punkt.

Evtl. Hast du eine Vorstellungskraft und kannst dir einen Pfeil vom einen zum anderen Punkt vorstellen.

---

Ja das schon. Aber darf man das einfach so? Also ich weiß echt nicht, wie ich das in ner Klausur machen soll