Hallo,
Muss man nun nach x auflösen? Wüsste nicht wie ich dabei vogehen soll.
Ja nach x auflösen. Das ist eine qudratische Gleichung. Du kennst sicher die Mitternachtsformel ;-) das gibt dann:$$\begin{aligned} \vec a \cdot \vec b &= |\vec a| \cdot |\vec b| \cdot \cos\left( \angle \vec a \vec b\right)\\ 6 + 3x &= \sqrt{6^2 + 3^2} \cdot \sqrt{1^2+x^2} \cdot \frac 12 \sqrt 2 \\ 6^2 + 36x + 9x^2 &= 45(1+x^2) \cdot \frac 12 \\ 0 &= 27x^2 -72x - 27 \\ x_{1,2} &= \frac{72 \pm \sqrt{72^2 - 4\cdot 27 \cdot (-27)}}{2 \cdot 27} \\ &= \frac{8 \pm \sqrt{8^2 + 36}}{6} \\ &= \frac{4 \pm 5}{3} \\ \end{aligned}$$
Du kannst es Dir aber auch einfacher machen.
Es ist offensichtlich so, dass es zwei Lösungen gibt. \(\vec b\) kann ja auf beiden Seiten von \(\vec a\) liegen.
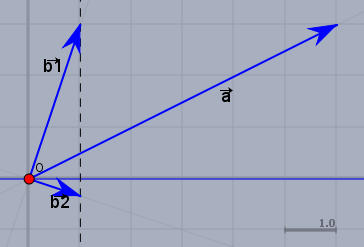
Und da der Winkel zu \(\vec a\) 45° beträgt, so muss der Winkel zwischen den beiden Lösungsvektoren \(\vec b_{1}\) und \(\vec b_2\) 90° betragen. D.h. ihr Skalarprodukt ist gleich 0. Es muss also gelten:$$\vec b_1\cdot \vec b_2 = 1+x_1x_2 = 0 \implies x_2 = -\frac 1{x_1}$$und beim Skalarprodukt mit \(\vec a\) muss in beiden Fällen der gleiche Winkel heraus kommen. Folglich ist$$\begin{aligned}\frac{\vec a\vec b_1}{|\vec a ||\vec b_1|} &= \frac{\vec a \vec b_2}{|\vec a|| \vec b_2|} \\\frac{\vec a\vec b_1}{|\vec b_1|} &= \frac{\vec a \vec b_2}{| \vec b_2|} \\ \frac{6+3x_1}{\sqrt{1+x_1^2}} &= \frac{6 - \frac 3{x_1}}{\sqrt{1+ \frac 1{x_1^2}}} = \frac{6x_1 - 3}{\sqrt{x_1^2+ 1}} \\ 6+3x_1&= 6x_1-3 \\ x_1 &= 3 \implies x_2 = -\frac 13\end{aligned}$$