Hallo,
Ein solcher Spiegel ist eine Parabel. Und eine Parabel ist die Menge aller Punkte, die von einem Punkt (dem Brennpunkt) und einer Geraden (der Leitgeraden) den gleichen Abstand haben.
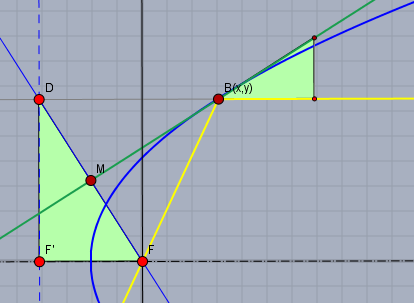
Oben ist daher immer \(|DB|=|FB|\) und die grüne Tangente ist die Mittelsenkrechte der Strecke \(DF\). Umgekehrt verläuft jedes Bild eines horizontal einfallenden Lichtstrahls, der an der Tangente gespiegelt wird, durch den Brennpunkt \(F\).
Zeichnet man das Steigungsdreieck für die Tangente an die Parabel im Punkt \(B(x,\,y)\), so findet man ein ähnliches Dreieck \(\triangle F'FD\). Es sei \(|F'F| = p\) dann gilt für die Steigung \(y'\) der Tangente$$y' = \frac py$$
Die Lösung der DGL gibt $$\begin{aligned} y' &= \frac py \\ \frac{\text dy}{\text dx}y &= p \\ y \text dy&= p \text dx\\ \int y \text dy&= \int p \text dx\\ \frac 12 y^2 &= px + C \\ y^2 &= 2px + 2C \\ \end{aligned} $$Damit der Brennpunkt auch in den Ursprung rückt, muss gelten: \(y(-p/2) = 0\)$$y\left(-\frac p2\right) = 0 \\ \implies 0=2p \cdot\left(-\frac p2\right)+ 2C \implies C = \frac 12 p^2 \\ y^2 = 2px +p^2 = 2p\left(x+\frac p2\right) $$Gruß Werner