Bestimmen von Funktionsterm der Wahrscheinlichkeitsdichte

Question

Aufgabe:

Eine stetige Zufallsgröße X ist auf dem Intervall [2;10] definiert und besitzt als Wahrscheinlichkeitsdichte eine lineare Funktion mit f(x)=m*x+c. Für den Erwartungswert von X gilt u=8. Bestimmen Sie den Funktionsterm von f.

Problem/Ansatz:

Wie berechnet man das?

Muss ich die Funktion mit dem Erwartungswert berechnen?

Answer 1

Hallo,

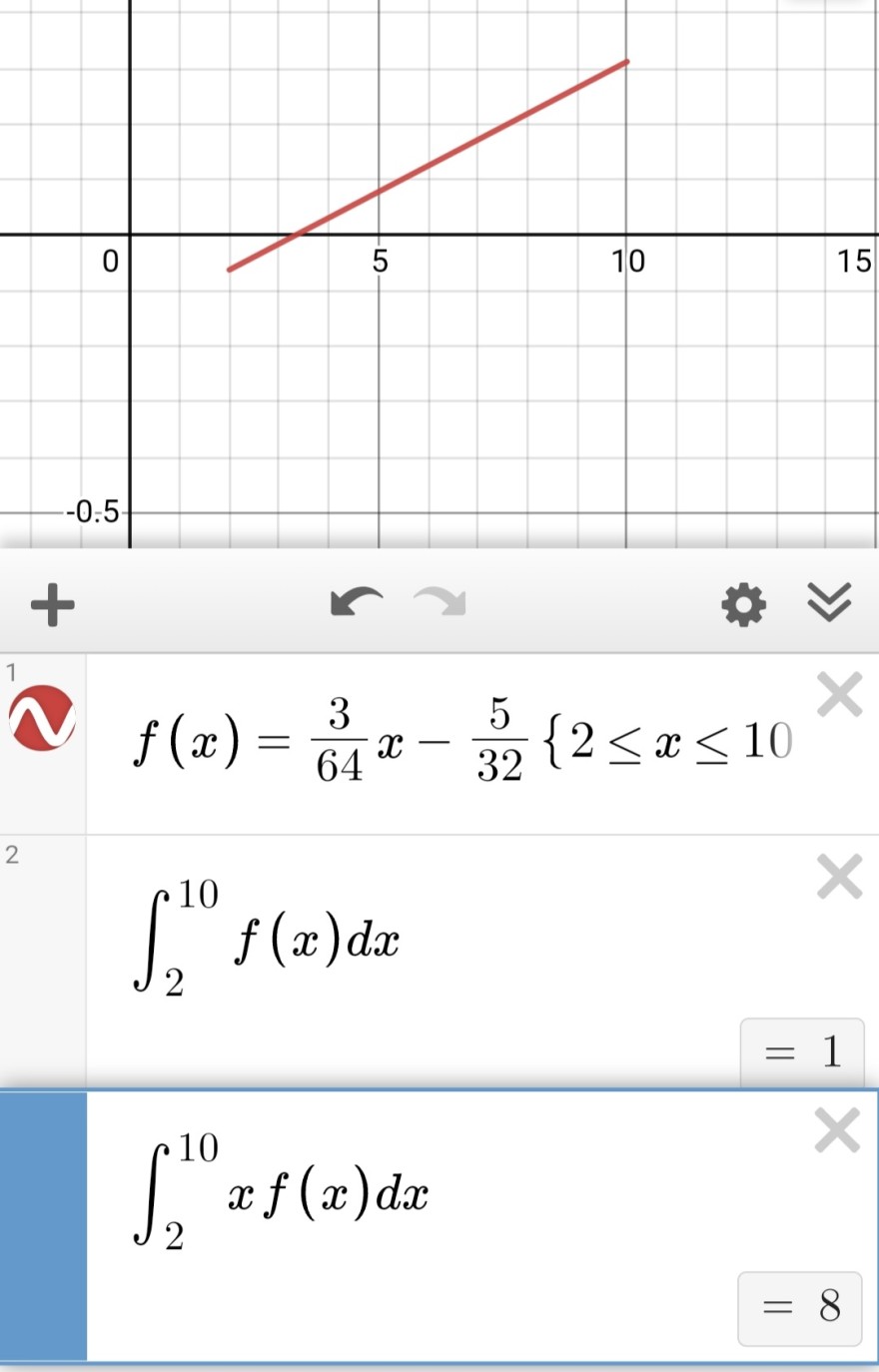
der Inhalt der Fläche unter der Geraden im gegebenen Intervall muss 1 sein.

Nun muss noch der Erwartungswert 8 verwendet werden.

Damit hast du zwei Gleichungen und kannst m und c bestimmen.

:-)

PS

Die Lösung kann nicht richtig sein, da die Dichtefunktion keine negativen Werte annehmen darf.

Comments

Ich hatte das eigentlich so gemacht

\( \int\limits_{2}^{10} \)mx+cdx= [ 1/2 mx² +cx ] = [ 1/2 m10²+c10] - [ 1/2 m2²+2c] = 

48m+8c =1 /-8c

48m=1-8c / :48

m

---

Das sieht doch schon gut aus.

Nun musst du noch den Erwartungswert 8 ausnutzen.

---

\( \int\limits_{2}^{10} \) x•(mx+c)dx= mx² +cx = [ 1/3mx³ + 1/2cx^{2 ].}

⁼ [ 1/3 m 10^3 + 1/2c10^2]…

= [1000/3m+50c]- [ 8/3m + 2c]

= 992/3m+48c=8

Und wie muss ich jetzt vorgehen um auf f zu kommen?

---

Jetzt hast du zwei Gleichungen und kannst m und c berechnen.

m=3/64

c=-5/32

---

Also habe ich jetzt die zwei Gleichungen:

48m+8c=1

992/3m+48c=8

Wenn ich bei der ersten Gleichung nach m Auflöse habe ich m= 1/48-1/6c

Das setze ich dann in die zweite Gleichung ein, jedoch kommen ganz andere Ergebnisse raus als bei Ihnen.

Könnten Sie mir bitte den Rechenfehler zeigen?

danke für ihre Hilfe!

---

48m+8c=1 → -288m-48c=-6

992/3m+48c=8

Addieren:

m*(-288+992/3)=2

m*128/3=2m=3/64

Da du nicht deine weiteren Rechenschritte angibst, weiß ich nicht, welchen Fehler du machst.

---

Vielen Dank!