Bestimmen Sie die lokalen Extremstellen der folgenden Funktionen (mehrdimensional)

Question

Bestimmen Sie die lokalen Extremstellen der folgenden Funktionen:

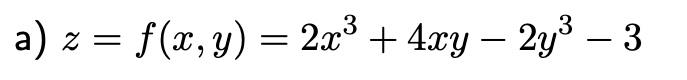
Text erkannt:

a) $z=f(x, y)=2 x^{3}+4 x y-2 y^{3}-3$

Die ersten beiden partiellen Ableitungen bekomme ich noch hin, doch wie geht es von da aus weiter? Wie findet man die Extremstellen?

Hab die beiden Gleichungen schon versucht umzustellen, aufzulösen, einzusetzen... doch ich habe keine Ahnung, wie man jetzt auf die Extremstellen kommt...

Laut Lösung liegen die bei (2/3 , -2/3 )

Was sagt das jetzt genau aus? Und wie macht man von da aus weiter?

Answer 1

Aloha :)

Kandidaten für Extremstellen der Funktion$$f(x;y)=2x^3+4xy-2y^3-3$$findest du dort, wo der Gradient $=\vec 0$ wird:$$\binom{0}{0}\stackrel!=\operatorname{grad}f=\binom{6x^2+4y}{4x-6y^2}\implies4y=-6x^2\;\land\;4x=6y^2\implies y=-\frac32x^2\;\land\;x=\frac32y^2$$Weil Quadratzahlen nie negativ sein können, ist klar, dass $y\le0$ und $x\ge0$ sein muss. Wir erkennen auch sofort die triviale Lösung $(0;0)$. Es gibt aber noch eine Lösung:$$x=\frac32y^2=\frac32\left(-\frac32x^2\right)^2=\left(\frac32\right)^3x^4\stackrel{x>0}{\implies}1=\left(\frac32x\right)^3\implies x=\frac23\implies y=-\frac23$$Wir haben also zwei Kandidaten gefunden:$$K_1(0|0)\quad;\quad K_2\left(\frac23\bigg|-\frac23\right)$$

Zur Bestimmung der Art der Extrema bestimmen wir die Hesse-Matrix:$$H(x;y)=\left(\begin{array}{rr}12x & 4\\4 & -12y\end{array}\right)$$Die Eigenwerte von $H(0;0)$ sind $\pm4$. Daher ist die Hesse-Matrix am Punkt $(0|0)$ indefinit, sodass kein Extremum vorliegt. Für $H(\frac23;-\frac23)$ lauten die Eigenwerte $4$ und $12$, also ist die Hesse-Matrix im Punkt $(\frac23|-\frac23)$ positiv definit, sodass bei diesem Punkt ein Minimum vorliegt.