Moin,
Ich habe eine Frage, bezüglich dieser Aufgabe. Könnte mir jemand erklären wie man vom oberen auf die 2. Zeile kommt? Weil wenn ich das (wie üblich bei diesen potenze) mit dem paslcalschen Dreieck löse, komme ich nie auf diese Zahlen.
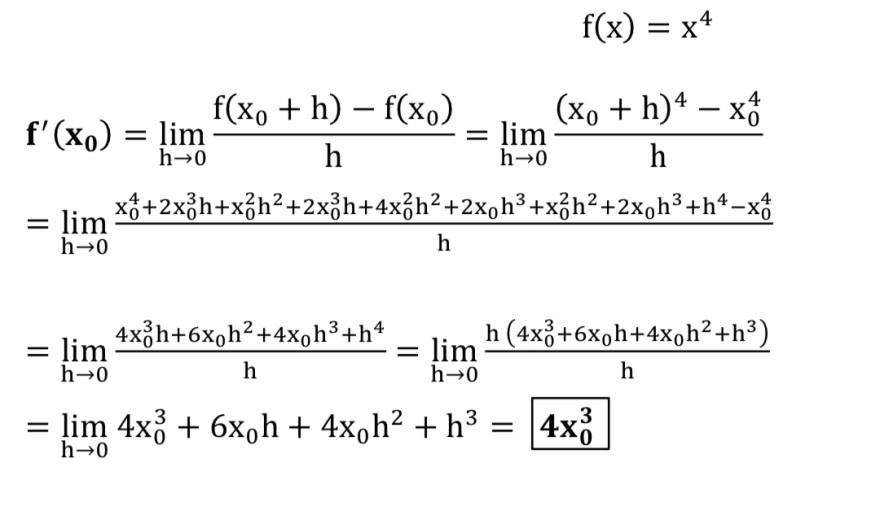
Text erkannt:
\( f^{\prime}\left(x_{0}\right)=\lim \limits_{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}=\lim \limits_{h \rightarrow 0} \frac{\left(x_{0}+h\right)^{4}-x_{0}^{4}}{h} \)
\( =\lim \limits_{h \rightarrow 0} \frac{x_{0}^{4}+2 x_{0}^{3} h+x_{0}^{2} h^{2}+2 x_{0}^{3} h+4 x_{0}^{2} h^{2}+2 x_{0} h^{3}+x_{0}^{2} h^{2}+2 x_{0} h^{3}+h^{4}-x_{0}^{4}}{h} \)
\( =\lim \limits_{h \rightarrow 0} \frac{4 x_{0}^{3} h+6 x_{0} h^{2}+4 x_{0} h^{3}+h^{4}}{h}=\lim \limits_{h \rightarrow 0} \frac{h\left(4 x_{0}^{3}+6 x_{0} h+4 x_{0} h^{2}+h^{3}\right)}{h} \)
\( =\lim \limits_{h \rightarrow 0} 4 x_{0}^{3}+6 x_{0} h+4 x_{0} h^{2}+h^{3}=4 x_{0}^{3} \)
Danke für antworten schonmal ;)
Text erkannt:
\( f^{\prime}\left(x_{0}\right)=\lim \limits_{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}=\lim \limits_{h \rightarrow 0} \frac{\left(x_{0}+h\right)^{4}-x_{0}^{4}}{h} \)
\( =\lim \limits_{h \rightarrow 0} \frac{x_{0}^{4}+2 x_{0}^{3} h+x_{0}^{2} h^{2}+2 x_{0}^{3} h+4 x_{0}^{2} h^{2}+2 x_{0} h^{3}+x_{0}^{2} h^{2}+2 x_{0} h^{3}+h^{4}-x_{0}^{4}}{h} \)
\( =\lim \limits_{h \rightarrow 0} \frac{4 x_{0}^{3} h+6 x_{0} h^{2}+4 x_{0} h^{3}+h^{4}}{h}=\lim \limits_{h \rightarrow 0} \frac{h\left(4 x_{0}^{3}+6 x_{0} h+4 x_{0} h^{2}+h^{3}\right)}{h} \)
\( =\lim \limits_{h \rightarrow 0} 4 x_{0}^{3}+6 x_{0} h+4 x_{0} h^{2}+h^{3}=4 x_{0}^{3} \)