Aufgabe:
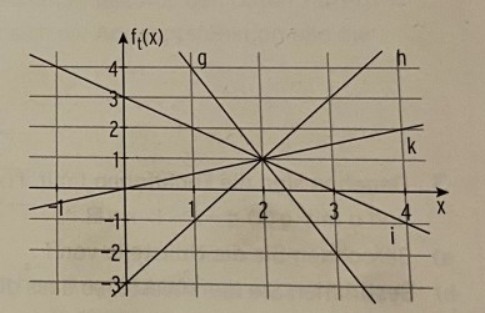
Die Abbildung zeigt die Schargeraden von \( f_{t} \) mit \( f_{t}(x)=0,5 t x-(t-1) \quad ; x, t \in \mathbb{R} \), für verschiedene Werte von \( t \). Ordnen Sie jeder Geraden einen passenden Parameterwert zu.
Bestimmen Sie Werte für t, sodass die zugehörige Gerade für \( x \geq 0 \) eine Erlösgerade sein könnte.
Problem/Ansatz:
Hallo zusammen!,
Ich wollt fragen, ob ich diese Aufgabe richtig gelöst habe
meine Parameterwerte sind:
g: t=-3
h: t=2
K: t=0,5
i: t=-1
Allerdings weißt ich nicht ganz genau was man bei der darauffolgenden Aufgabe machen soll, ich hätte jetzt gedacht das man vielleicht in der Funktionsgleichung ft(x), x=1 einsetzt, da man ja dann auf 0,5x kommt.