Guten Tag mathef
Danke vielmals für die schnelle Antwort.
Wie kommt man auf x = u2-1?
Mein Rechnungsweg sieht so aus:
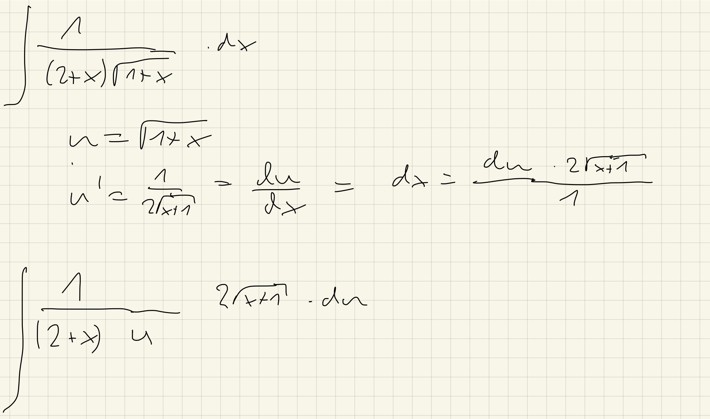
Text erkannt:
\( \int \frac{1}{(2+x) \sqrt{1+x}} \cdot d x \)
\( u=\sqrt{1+x} \)
\( u^{\prime}=\frac{1}{2 \sqrt{x+1}}=\frac{\ln }{d x}=d x=\frac{d u}{1} \cdot \frac{2 \sqrt{x+1}}{1} \)
\( \int \frac{1}{(2+x) u} 2 \sqrt{x+1} \cdot d u \)