Bestimme mit Hilfe des Schaubilds näherungsweise eine stelle x_{0} an der die Ableitung f^{\prime}(x_{0})=-1 ist?

Question

Aufgabe:

Ist das richtig so ?

Text erkannt:

Autgabe: \( (1 \) punkt \( ) \) Im Schaubild sieht man den Graph der Funktion f.

Bestimme mit Hilfe des Schaubilds näherungsweise eine stelle \( x_{0} \) an der die Ableitung \( f^{\prime}\left(x_{0}\right)=-1 \) ist.

Problem/Ansatz:

Comments

Was sollen deine Doppel-Posts?

---

Hallo Monty,

in der anderen Aufgabe ist aber von -1,3
und einem anderen Schaubild die Rede.

---

Die hat er ja auch zweimal gepostet.

Answer 1

Nein.........................................

Comments

jetzt bin ich aber komplett verwirrt

Answer 2

Hallo King,

tan ( a ) = -1
a = 45 ° abwärts / fallend

Comments

was ist dann x0 ?

---

Die Hypotenuse eines Geodreiecks hat den Winkel -45 °

Du setzt ein Geodreick mit den Katheten
parallel zu den Koordinatenachsen
an

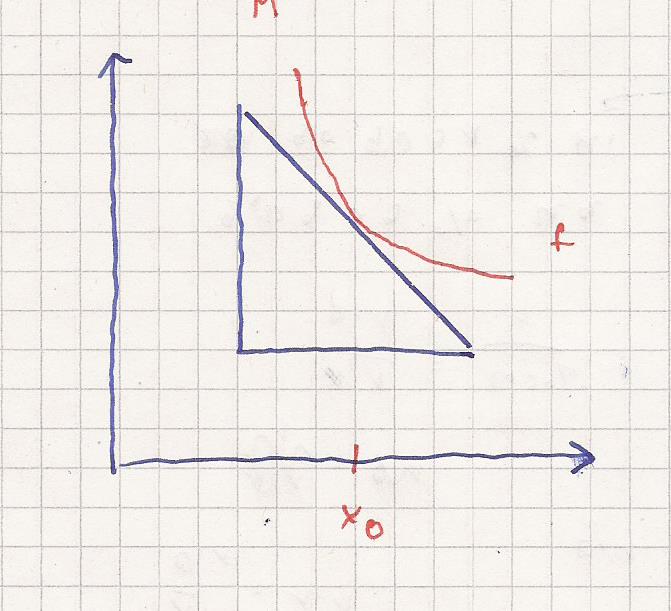
Dann verschiebst du das Geodreieck an die Kurve f.
Der Andockpunkt hat die Steigung = -1

Die x-Stelle des Andockpunkts ist x0.

---

also ist x0= -1

---

Der Punkt x0 = -1 hat die Steigung 0
( Extrempunkt Hochpunkt )

Der Punkt x0 = 1.5 hat etwa die
Steigung - 1.

Answer 3

Gesucht ist eine Stelle auf deinem Graphen mit einer Steigung von -1.

An der Stelle x=-1 hast du eine lokale Extremstelle, also f '(x) = 0.

Comments

also ist x0= 1

---

Hallo paddi,
es wurde aber nicht der Punkt mit der
Steigung 0 gesucht
sondern
mit der Steigung -1.

mfg Georg

---

Hallo Georg, er hat aber gefragt ob seine Lösung x= -1 richtig ist.

---

So eine Frage sehe ich aber nicht.
Er hat bei dir gefragt
also ist x0= 1

---

Ich beziehe mich auf die Fragestellung im Post.

MfG paddi.