Aus (2x)^x wird ln(2x) * x, aber wieso?

Question

Aufgabe:

\(\lim \limits_{x \rightarrow 0}(2 x)^{x} \rightarrow \lim \limits_{x \rightarrow 0} \ln (2 x) \cdot x \)

Problem/Ansatz:

Ich bin gerade auf diese Aufgabe gestoßen und verstehe nicht, wieso man diesen Term anders schreiben kann, also zu ln(2x) * x.

Wieso ist es mathematisch korrekt (2x)^x zu ln(2x) * x zu schreiben.

Comments

Da fehlt ein e hoch dein ln Ausdruck. Und das ist auch nicht für alle x im allgemeinen korrekt

---

meinst du das hier: $$e^{ln(2x)*x}$$

Aber aus $$e^{ln(2x)*x}$$ wird ja nicht $$(2x)^x$$

Answer 1

$$ (2x)^x = e^{\ln(2x) \cdot x} = \exp{ \left( \frac{\ln(2x)}{ \frac{1}{x} } \right) }$$

Und jetzt L'Hospitall auf den Exponenten anwenden.

Comments

Das mit L 'Hospitall ist mir bewusst, wie man das macht, ich verstehe nur nicht die Äquivalenz zwischen (2x)^x = \(e^{ln(2x)*x}\) .

Warum wird aus (2x)^x <-> \(e^{ln(2x)*x}\).

und nicht aus (2x)^x <-> \(e^{ln(2x)^x}\).

---

$$ x \ln(2x) = \ln(2x)^x $$ also $$ \exp \left(x \ln(2x) \right) = (2x)^x $$

---

Achso okay. Danke jetzt hab ichs verstanden :)

.

Answer 2

Ich habe die Diskussion etwas verfolgt
Zunächst : e und ln sind Umkehrfunktionen
und heben sich auf

e hoch ( ln z ) = z

um zu einem Ergebnis für ( 2x ) hoch x zu kommen
wird ersetzt

e hoch ( ln ( ( 2x ) hoch x ) )
e hoch ( x * ln ( 2x ) )
e hoch wird zunächst weggelassen
x * ln ( 2x ) wird umgeformt zu
ln ( 2x ) / ( 1/x )
dann für
lim x -> 0  [ ln ( 2x ) / ( 1/x ) ] =  ∞ / ∞

Ein Fall für´s Krankenhaus
ln ( 2x ) ´ / ( 1/x ) ´

( 1/x ) / ( - 1/x^2 )
1/x * x^2 /( -1)
- x
lim x - > 0 [ -x ] = 0

wieder retoure :
e hoch wird zunächst weggelassen

e^ 0 = 1

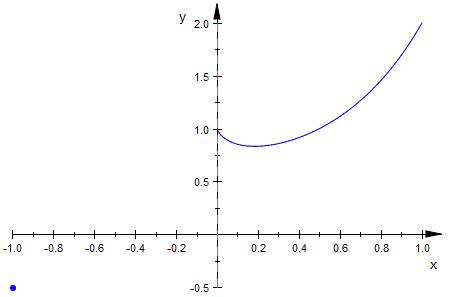
Der Graph der Funktion ( ( 2x ) ^x )

Comments

Okey, das war echt eine bessere Antwort und zu 100% nachvollziehbar :)

Danke dir für deine Mühe, habe es jetzt besser verstanden.

"Zunächst : e und ln sind Umkehrfunktionen
und heben sich auf

e hoch ( ln z ) = z"

Das hat echt geholfen.

---

Schön das dir geholfen werden konnte.