Welches Volumen nimmt der so entstehende Zylinder ein?

Question

Aufgabe:

Hallo, ich komme bei der Aufgabe 8 nicht weiter.

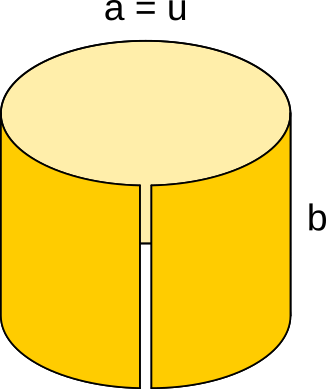
Ein rechteckiger Papierstreifen mit den Seitenlängen a = 50 cm und b = 14 cm wird entlang der Seite a zu einem Kreis gebogen. Welches Volumen nimmt der so entstehende Zylinder ein? Trage den ganzzahligen Wert der Lösung ein.

Problem/Ansatz:

Ich habe es versucht, aber es zeigt mir ständig eine anderes Lösung an. Wie könnte ich es berechnen?

Answer 1

Ich habe es versucht,

Davon sehe ich nichts.

Berechne aus dem Umfang a den Kreisradius.

(Es gilt u=2πr).

Berechne aus dem Kreisradius die Kreisfläche.

(Es gilt A=πr².)

Multipliziere die Kreisfläche mit der Höhe b.

Comments

Vielen Dank :)

Answer 2

Hallo,

Das Volumen eines Zylinders berechnest du mit \(V=\pi\cdot r^2\cdot h\), also Grundfläche mal Höhe.

Die Seite a ist der Umfang \(U=2\cdot\pi\cdot r=50\) des Zylinders. Damit kannst du r berechnen.

Den Rest schaffst du bestimmt alleine, sonst melde dich.

Gruß, Silvia

Answer 3

Ein rechteckiger Papierstreifen mit den Seitenlängen a = 50 cm und b = 14 cm wird entlang der Seite a zu einem Kreis gebogen.

U=2*r*π     50=2*r*π     r=\( \frac{25}{π} \)

V=r^2*π*h   wobei h=b    V= r^2*π*b   V=\( \frac{25^2}{π^2} \)*π*14

V=\( \frac{625}{π} \)*14=\( \frac{8750}{π} \) \( cm^{3} \)

Answer 4

Hallo,

[spoiler]

\(a=2\pi r~~~;~~~b=h\\ r=\dfrac{a}{2\pi}\\r^2=\dfrac{a^2}{4\pi^2}\\ V=\pi r^2 h \\=\dfrac{a^2\cdot b}{4\pi}\\=\dfrac{50^2\cdot 14}{4\pi}\text{ cm}^3\\=\dfrac{ 8750}{\pi} \text{ cm}^3\\ \approx 2785\text{ cm}^3\)

[/spoiler]

:-)