Aufgabe:
Beweisen oder widerlegen Sie:
Jeder vollständige Verband ist endlich.
Problem/Ansatz:
Müsste falsch sein, zumindest steht überall im Internet das jeder endliche Verband auch vollständig ist. Deshalb gehe ich davon aus das wenn es nicht explizit gesagt wird, die Gegenrichtung nicht zwingend der Fall ist. Aber wie Beweise ich das. Ich brauche eigentlich nur ein Gegenbeispiel für einen vollständigen Verband der unendlich ist, oder? kann mir da jemand helfen?
Wäre zb die total geordnete Menge ℕ ein vollständiger Verband der unendlich ist? Ich glaube eigentlich ℕ ist kein Vollständiger Verband.
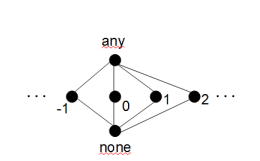
Wäre dieser flache Verband der ganzen Zahlen ein vollständiger Verband der unenglich ist: ?