Steigung von Tangente an Parabel

Question

Aufgabe: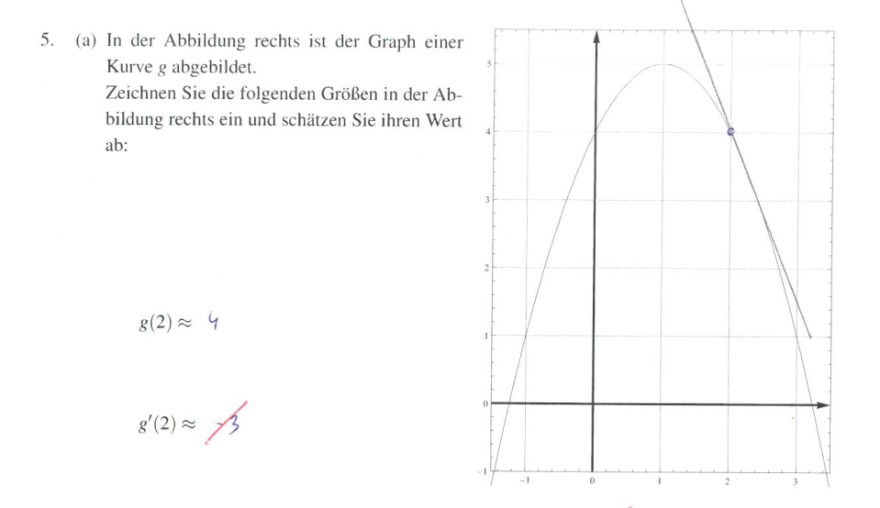

Text erkannt:

5. (a) In der Abbildung rechts ist der Graph einer Kurve \( g \) abgebildet.
Zeichnen Sie die folgenden Größen in der Abbildung rechts ein und schätzen Sie ihren Wert ab:
\( g(2) \approx 4 \)

Problem/Ansatz:

Ich verstehe nicht worin der Fehler besteht? Soweit ich weiß,ist eine Tangente eine Gerade, für die Bestimmung deren man von dem Berührungspunkt einmal nach rechts geht und dann runter. Bitte erklärt ihr mir. Inniger Dank!

Answer 1

eine Gerade, für die Bestimmung deren man von dem Berührungspunkt einmal nach rechts geht und dann runter

So bestimmt man die Steigung der Graden, nicht die Gerade selbst.

Ich schätze eher -2,5

Answer 2

ist eine Tangente eine Gerade, für die Bestimmung deren man von dem Berührungspunkt einmal nach rechts geht und dann runter.

Diese Aussage verstehe ich nicht. Wie bist Du auf -3 gekommen?

Die Funktion g ist g(x) = -x²+2x+4, die erste Ableitung dann g'(x) = -2x+2, g'(2) kannst Du damit ausrechnen. Die falsch eingezeichnete Tangente hätte eine Steigung von etwa -2,5.

Comments

Hier noch eine Skizze zur Erklärung:

Answer 3

Steigung m = (4-3)/(2-2,4) = -2,5

2,4 ist geschätzt

Answer 4

Für die Schätzung von g'(2) kann man auch zunächst die Gleichung der Parabel schätzen: f(x)= - (x - 1)²+5.

Comments

Dann gilt für f(x)=3

-(x-1)^2+5 = 3

(x-1)^2 = 2

x-1 = √2+1 = -2,41 

---

War nur eine Schätzung.