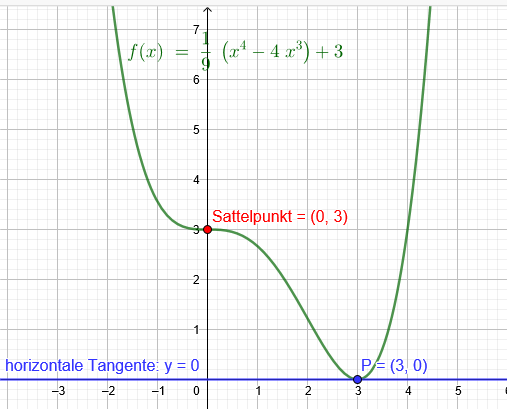
"Aufgabe: Bestimme eine ganzrationale Funktion 4.Grades, für die gilt
S(0|3) ist Sattelpunkt, im Punkt P(3|0) liegt eine horizontale Tangente vor."
Ich verschiebe den Graphen um 3 Einheiten nach unten: S´(0|0)(-> ist eine Dreifachnullstelle) ; P´(3|-3) und mache weiter mit der Nullstellenforn der Parabel 4.Grades
f(x)=a*x^3*(x-N)
P´(3|-3)
f(3)=3^3*a*(3-N)=27a*(3-N)
1.)27a*(3-N)=-3 9a*(3-N)=-1 9a*(N-3)=1 a=\( \frac{1}{9*(N-3)} \)
f(x)=\( \frac{1}{9*(N-3)} \)*[x^4-x^3*N]
horizontale Tangente bei P´(3|-3):
f´(x)=\( \frac{1}{9*(N-3)} \)*[4x^3-3*x^2*N]
f´(3)=\( \frac{1}{9*(N-3)} \)*[4*3^3-3*3^2*N]
\( \frac{1}{9*(N-3)} \)*[108-27*N]=0 N=4 a=\( \frac{1}{9*(4-3)} \)=\( \frac{1}{9} \)
f(x)=\( \frac{1}{9} \)*[x^4-4x^3]
Nun wieder 3 Einheiten nach oben:
p(x)=\( \frac{1}{9} \)*[x^4-4x^3]+3