Stellen Sie H‘ in Koordinatenform auf.
Die Ebene \(H'\) wird durch die drei Punkte \(D'=A\), \(P'\) und \(Q'\) definiert. Da \(D'=A\) der Urspung ist, reicht es hier aus, einen Normalenvektor \(\vec n\) aus dem Kreuzprodukt von \(AP'\) und \(AQ'\) zu berechnen. $$a\cdot \vec n = \begin{pmatrix}8\\ 7\\ -2\end{pmatrix} \times \begin{pmatrix}1\\ 11\\ -7\end{pmatrix} = \begin{pmatrix}-27\\ 54\\ 81\end{pmatrix}, \quad a \in \mathbb R$$wählt man \(a=27\), so wird \(\vec n\) zu$$\vec n = \begin{pmatrix}-1\\ 2\\ 3\end{pmatrix}$$Da der Ursprung in der Ebene liegt, wird die linke Seite der Koordinatenform zu \(0\). Also ist \(H'\)$$H':\quad \begin{pmatrix}-1\\ 2\\ 3\end{pmatrix} \vec x = 0 \quad\Leftrightarrow\quad-x_1+2x_2+3x_3=0$$Zur Kontrolle das ganze in Geoknecht3D
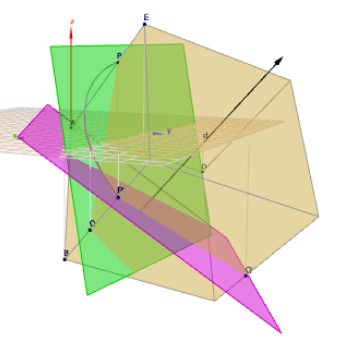
\(H'\) ist die lila Ebene. Der schwarze Vektor ist die Drehachse der Schichten 1 und 2 aus der Aufgabenstellung.
Bestimmen Sie den Drehwinkel von H nach H‘.
Kommt drauf an, welche Drehachse gemeint ist! Nimmt man die vorgegebene Drehachse aus der Aufgabenbestellung, so kann man \(H\) mit einer 90° um die eingezeichnete Drehachse (s. Bild) in \(H'\) überführen.
Ist dagegen nach dem Winkel \(\alpha\) zwischen den Ebenen gefragt, so ist dieser identisch mit dem Winkel zwischen den Normalenvektoren. Zu berechnen aus dem Skalarprodukt:$$\cos(\alpha) = \frac{\left|\vec n \cdot \vec n_H\right|}{|\vec n|\cdot|\vec n_H|} =\frac{\begin{pmatrix}-1\\ 2\\ 3\end{pmatrix} \cdot \begin{pmatrix}1\\ 11\\ 2\end{pmatrix}}{\left|\begin{pmatrix}-1\\ 2\\ 3\end{pmatrix}\right|\cdot\left|\begin{pmatrix}1\\ 11\\ 2\end{pmatrix}\right|}\\\phantom{\cos(\alpha)}= \frac{-1 + 22 + 6}{\sqrt{(-1)^2+ 2^2+3^2}\cdot\sqrt{1^2+11^2+2^2}} = \frac{27}{42}\\\implies \alpha\approx 50°$$\(\vec n_H\) ist ein Normalenvektor von \(H\), dem man aus der Koordinatenform von \(H\) ablesen kann.
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner