Erstmal sorry für meine folgenden Zeichnungen...ich hoffe, Du kannst es trotzdem nachvollziehen.
Der von Dir gezeigte doppelte Stöpsel ist auf der Spitze gespiegelt, ähnlich einer Sanduhr.
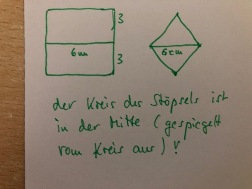
Das führt dazu, dass er, neben dem Kreis, durch EIN Rechteck passt....1 Rechteck. wenn man ihn etwas staucht, also auf 3 cm Höhe ( das ist auf deinem Bild jetzt nicht so zu sehen ) auch durch EIN Quadrat, okay. Die Aufgabenstellung war aber, dass er durch zwei...2 Quadrate ( einmal 6 cm Kantenlänge und einmal 6 cm Diagonale ) passen und diese auch vollständig ausfüllen muss. Deshalb muss das Ganze auf der Linie des Kreises, also auf dem dicken Ende gespiegelt werden. Das ergibt dann auch 2 Dreiecke, die mit einer Höhe von 3 cm aneinander ein weiteres Quadrat bilden, und zwar das kleinere mit 6 cm Diagonale. So habe ich in den 3 Dimensionen den Kreis und beide Quadrate komplett abgedeckt. Mit der Spiegelung von Dir klappt das nicht. Die rechte Zeichnung ist etwas zu klein geraten, aber damit ist deutlich sichtbar, dass einmal das Quadrat mit 6 cm Kantenlänge und auch das kleinere Quadrat mit 6 cm Diagonale abgedeckt wird ( letzteres durch das Aneinanderlegen von den 2 Dreiecken beider Stöpsel mit Grundlinie 6cm und Höhe 3 cm.
Jetzt zur Rechnung. Ich komme mit einer anderen Formel auf haarscharf das gleiche Ergebnis wie Du, was das Volumen angeht. Dafür spielt die Darstellung als Sanduhr oder als Brummkreisel ja auch keine Rolle. Also alles bestens...Hier meine Formel für das Volumen.
Text erkannt:
der Vreis des stopsels ist in der Hithe (gespicget rour Kreis aus)

Text erkannt:
\( V=1 / 3 \cdot\left(3 \cdot p_{i}-4\right) \cdot h \cdot t^{2} \)
\( V=1 / 3 \cdot(5,42477) \cdot 3 \cdot 9 \)
\( V=1 / 3 \cdot 489,146,46879 \)
\( V=48,82293 \times 2 \)
\( V=97,64586 \)
\( V \approx 97,646 \)
Jetzt zur Oberfläche. Da Deine Version auf der Spitze gespiegelt ist musst Du bei der Berechnung der Gesamtoberfläche die Oberfläche des einfachen Stöpsels einfach nur mal 2 nehmen, sprich verdoppeln. Du hast da 195,818 raus. Leider ist keine Formel dabei, wie Du auf dieses Ergebnis kommst.
Ich habe jetzt von einem Bekannten die Lösung für die Oberfläche bekommen....die er mittels eines Computerprogrammes für den 3 D Drucker ermittelt hat. Und die ist 121,069 und weicht somit total von Deinem Ergebnis ab.
Grund dafür ist, dass ich bei der Spiegelung über die Achse des Kreises bei der Berechnung der Oberfläche nicht den einfachen Stöpsel mal 2 nehmen kann, wie bei Deiner Spiegelung über die Spitze. Bei Dir liegen alle Oberflächen frei und müssen bei der Berechnung der Oberfläche berücksichtigt werden. Bei meiner Version verschwindet die Kreisfläche komplett im Körper und darf somit bei der Berechnung der Oberfläche nicht mit einbezogen werden. Denn die Oberfläche des Kreises wird ja beidseitig ( mittig und innen) genutzt. Deshalb muss ich bei der Berechnung der Gesamtoberfläche des Doppelstöpsels die Oberfläche des Kreises komplett vernachlässigen.
Welche Formel hast Du denn für die Berechnung der Oberfläche genutzt?
Ich habe gedacht, wenn ich von Deinem Ergebnis jetzt 2x die Oberfläche des Kreises abziehe, würde ich auf mein Ergebnis kommen, aber das passt leider auch nicht.
195,818 - ( 2x Oberfläche Kreis )
195,818 - 56,548 = 139,270cm²
Die korrekte Oberfläche ist 121,069cm² Quadratzentimeter.
Dahingehend müssen wir die Berechnung für die Gesamtoberfläche des über die Kreisachse gespiegelten Stöpsels verändern.
Wenn bis jetzt alles klar ist dürfte dieser letzte Schritt doch kein Problem mehr sein, oder hast Du Dein Ergebnis ( Mantel, Oberfläche ) auch über ein Computerprogramm erhalten?
Ich komme mit diesen Programmen ja überhaupt nicht klar und muss noch eine stinknormale Formel vor mir haben, damit ich auf ein Ergebnis komme. Bei der Berechnung des Volumens hat das ja prima geklappt....die Oberfläche bekommen wir beide doch jetzt auch noch hin, oder ??
LG