Graph einer Polynomfunktion von Grad 3

Question

Aufgabe:

Der graph einer polynomfunktion f grad 3 hat H=(-1/16) als hochpunkt und T=(3/-16) tiefpunkt. Man soll die Termdarstellung ermitteln.

Problem/Ansatz:

Ich habe alle bedingungen aufgestellt aber ich bekomme 4 gleichungen und ich weiss nicht mehr wie es weiter geht.

1. f(3)=-16

2. f‘(3)=0

3. f(-1)=16

4. f‘(-1)=0

Answer 1

1. f(3)=-16

2. f‘(3)=0

3. f(-1)=16

4. f‘(-1)=0

f(x)=a*x^3+b*x^2+c*x+d

1. f(3)=-16

f(3)=a*3^3+b*3^2+c*3+d          1.) 27a+9b+3c+d=-16

3. f(-1)=16

f(-1)=a*(-1)^3+b*(-1)^2+c*(-1)+d   3.) a*(-1)^3+b*(-1)^2+c*(-1)+d=16

f´(x)=3ax^2+2bx+c

2. f‘(3)=0

f´(3)=3a*3^2+2b*3+c    2.)  3a*3^2+2b*3+c=0

4. f‘(-1)=0

f´(-1)=3a(-1)^2+2b(-1)+c   4.) 3a(-1)^2+2b(-1)+c=0

Du hast nun 4 Gleichungen, (die du noch vereinfachen musst)  und 4 Unbekannte.

Comments

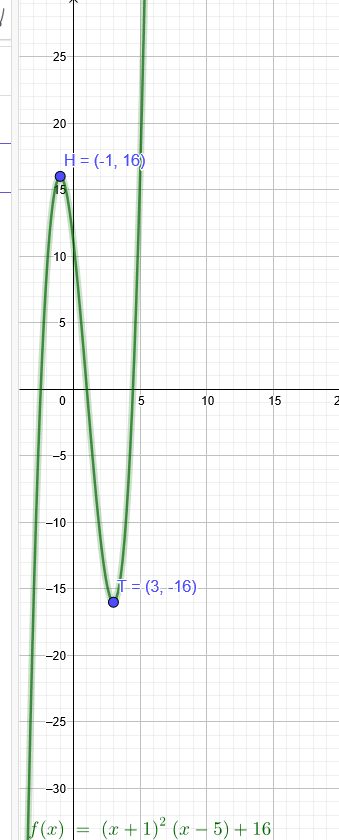
Der Graph einer Polynomfunktion f Grad 3 hat H=(-1|16) als Hochpunkt und T=(3|-16) als Tiefpunkt. Man soll die Termdarstellung ermitteln.

Ein anderer Weg:

Ich verschiebe den Graph von f(x) um 16 Einheiten nach unten und mache weiter mit der Nullstellenform der kubischen Parabel:

H´(-1|0) ist nun eine doppelte Nullstelle

f(x)=a*(x+1)^2(x-N)

T´(3|-32)

f(3)=a*(3+1)^2(3-N) =16a*(3-N)

1.) 16a*(3-N)=-32   a=\( \frac{-32}{16*(3-N)} \)=-\( \frac{2}{(3-N)} \)=\( \frac{2}{N-3} \)

Tiefpunkt hat waagerechte Tangente: Steigung m=0

f(x)=\( \frac{2}{N-3} \)*[(x+1)^2(x-N)]

f´(x)=\( \frac{2}{N-3} \)*[2*(x+1)(x-N)+(x+1)^2]

T´(3|...)

f´(3)=\( \frac{2}{N-3} \)*[2*(3+1)(3-N)+(3+1)^2]

\( \frac{2}{N-3} \)*[2*(3+1)(3-N)+(3+1)^2]=0

[2*(3+1)(3-N)+(3+1)^2]=0    N=5      a= \( \frac{2}{5-3} \)=1

f(x)=(x+1)^2(x-5)

Nun wieder  16 Einheiten nach oben verschieben:

p(x)=(x+1)^2(x-5)+16

---

Genau das hab ich auch eingesetzt in die gleichung und ich wollte fragen wie ich das jetzt löse also wie ich vorgehen muss

---

@M:

Du hast nun 4 Gleichungen, (...)

Stimmt, denn wie L es formuliert hat:

(...) ich bekomme 4 gleichungen (...)

---

1.)27a+9b+3c+d=-16  

2.)27a+6b+c=0

3.) -a+b-c+d=16  3.) d=16+a-b+c in 1.) einsetzen → I.)

4.)3a-2b+c=0

I.) 27a+9b+3c+16+a-b+c=-16  → I.) 28a+8b+4c=-32

→ I.) 7a+2b+c=-8

2.)27a+6b+c=0 

I.) 7a+2b+c=-8

2.)-I.): 20a+4b=8  → 2.)-I.): 5a+b=2  →2.)-I.): b=2-5a einsetzen in 4.)            und 2.)

4.)3a-2*(2-5a)+c=0      2.)27a+6*(2-5a)+c=0

4.)3a-4+10a+c=0         2.)27a+12-30a+c=0

4.)13a+c=4        2.)-3a+c=-12

4.)-2.):16a=16     a=1     2.)-3+c=-12    c=-9

2.)-I.): b=2-5     b=-3 

1.)27-27-27+d=-16      d=11

Die Alternative, die ich vorgerechnet habe, war für mich weniger anstrengend.

Answer 2

Ich habe alle bedingungen aufgestellt aber ich bekomme 4 gleichungen

Okay, das ist ja schon mal was. Es geht aber auch mit nur zwei Gleichungen! Denn weil die Graphen kubischer Funktionen stets symmetrisch zu ihrem einzigen, aber immer vorhandenen, Wendepunkt sind, lässt sich die Symmetrie bereits durch einen dem entsprechenden Ansatz ausnutzen, sofern der Wendepunkt bekannt ist. Da er hier die Mitte der Strecke HT bildet, hat er die Koordinaten (1|0).

Der Ansatz besteht nun darin, eine allgemeine, zum Ursprung symmetrische kubische Funktion zusammen mit ihrer Ableitung um eine Einheit nach rechts zu verschieben, also $$f(x)=a\cdot\left(x-1\right)^3+c\cdot\left(x-1\right)\\f'(x)=3 a\cdot\left(x-1\right)^2+c$$ Nun genügen die beiden Bedingungen \(f(3)=-16\) und \(f'(3)=0\), um zunächst \(c=-12\) und dann \(a=1\) zu bestimmen. Insgesamt ist das Ergebnis $$f(x)=\left(x-1\right)^3-12\cdot\left(x-1\right)$$ einfach in der Herleitung und zudem ansprechend in der Darstellung.