f(x)=\( \frac{x^2-1}{x^3-3x^2+2x} \) x∉{0,1,2,3}
In der Lösung dieser Aufgabe wird gesagt, dass die Funktion u.a. nicht in 0 und 2 stetig ist, da die Grenzwerte dieser Punkte nicht existieren. Wieso existieren die Grenzwerte nicht?
| 0 | 1 | 2 | 3 |
\( \frac{x^2-1}{x^3-3x^2+2x} \)
| -\( \frac{1}{0} \)
| \( \frac{0}{0} \)
| \( \frac{3}{0} \)
| \( \frac{8}{6 } \)
|
Hier siehst du, dass es nur bei x=3 einen Funktionswert gibt.
Bei x=1 kannst du die Regel von L´Hospital anwenden:
x→1 eingesetzt in \( \frac{2x}{3x^2-6x+2} \) ergibt -2
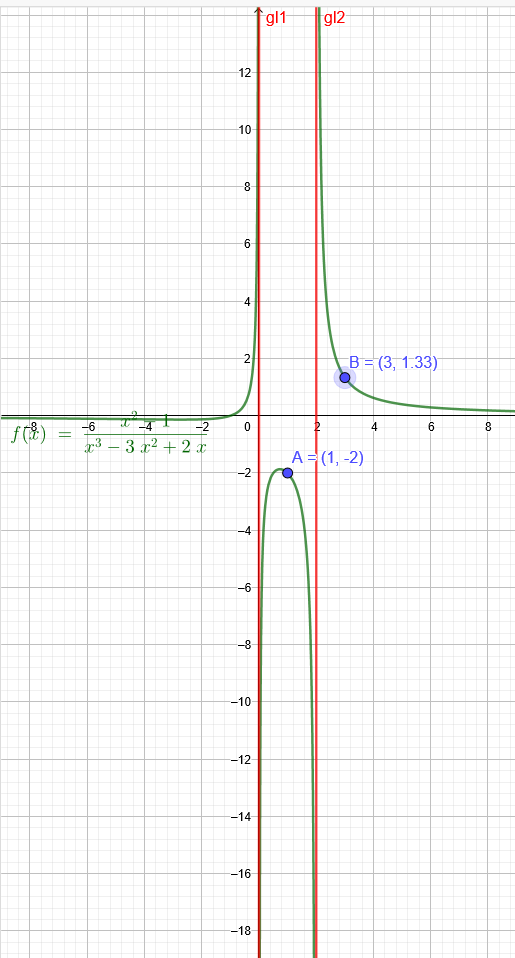
Die roten Geraden sind die beiden Pole.