Wie groß ist dieser Winkel, der von beiden Winkelhalbierenden gebildet wird.

Question

Aufgabe:

9. $\mathrm{ABC}$ soll ein rechtwinkliges Dreieck mit $\gamma=90^{\circ}$ sein; $\mathrm{M}$ soll der Mittelpunkt der Seite $\overline{\mathrm{AB}}$ sein. Konstruiere die Winkelhalbierenden von $\angle \mathrm{CMA}$ und von $\angle \mathrm{BMC}$.

Wie groß ist der Winkel, den diese beiden Winkelhalbierenden miteinander bilden? Begründe.

Problem/Ansatz:

Hätte ich gern NUR klein Tipp, wie gross dieser Winkel ,den von beiden Winkelhalbierenden gebildet wird.

ich denke ist 90 , weil diese is nur die Hälfte von 180 , als 90 . stimmt?

Answer 1

Die 90° und die Begründung sind richtig,

Comments

die Begründung ist falsch

Nein, das ist sie nicht.
Sie mag für manche Leute zu knapp sein, aber sie ist sicherlich korrekt., ein Thaleskreis verkompliziert die Sache jedenfalls nur unnötig.

---

ok las0o 90 stimmt? ok

ich habe Nur so geschriben, → " weil diese is nur die Hälfte von 180 , als 90 . stimmt?"

ich habe nicht geenit damit zu begründen. Laos du meinst mein Satz (( weil diese is nur die Hälfte von 180 , als 90 . stimmt?))) gilt auch las Begründung? Also ist die Aufgabe SCHON erledigt?

---

Hier ist die Begrünung im Buch:

Text erkannt:

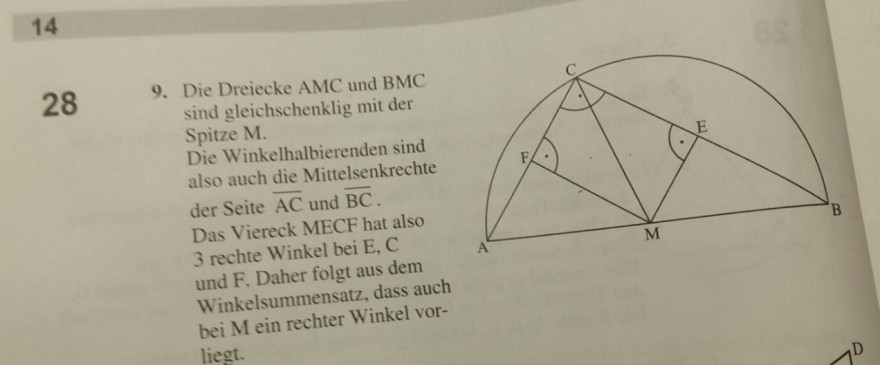
9. Die Dreiecke $\mathrm{AMC}$ und $\mathrm{BMC}$ sind gleichschenklig mit der Spitze M.
Die Winkelhalbierenden sind also auch die Mittelsenkrechte der Seite $\overline{\mathrm{AC}}$ und $\overline{\mathrm{BC}}$.
Das Viereck MECF hat also 3 rechte Winkel bei E, C und F. Daher folgt aus dem Winkelsummensatz, dass auch bei $M$ ein rechter Winkel vorliegt.

Jetzte meine Begründung

Ich begründe--> diese beide Winkel sind die Hälft vom Ganzen Winkel 180, daher sind sie zusammen 90((( lila Farbe )))). Also gine auch so meine Begründung?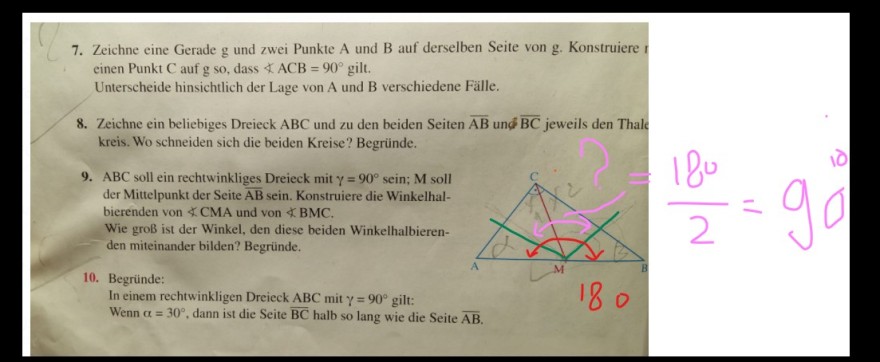

Text erkannt:

7. Zeichne eine Gerade $\mathrm{g}$ und zwei Punkte A und B auf derselben Seite von g. Konstruiere einen Punkt C auf g so, dass $\angle \mathrm{ACB}=90^{\circ}$ gilt.
Unterscheide hinsichtlich der Lage von $A$ und $B$ verschiedene Falle.
8. Zeichne ein beliebiges Dreieck $\mathrm{ABC}$ und zu den beiden Seiten $\overline{\mathrm{AB}}$ un $\bar{\beta} \overline{\mathrm{BC}}$ jeweils den Thale kreis. Wo schneiden sich die beiden Kreise? Begründe.
9. $\mathrm{ABC}$ soll ein rechtwinkliges Dreieck mit $\gamma=90^{\circ}$ sein; $\mathrm{M}$ soll der Mittelpunkt der Seite $\overline{\mathrm{AB}}$ sein. Konstruiere die Winkelhalbierenden von $\angle \mathrm{CMA}$ und von $\angle \mathrm{BMC}$.
Wie groß ist der Winkel, den diese beiden Winkelhalbierenden miteinander bilden? Begründe.
10. Begründe:
In einem rechtwinkligen Dreieck $\mathrm{ABC}$ mit $\gamma=90^{\circ}$ gilt:
Wenn $\alpha=30^{\circ}$, dann ist die Seite $\overline{\mathrm{BC}}$ halb so lang wie die Seite $\overline{\mathrm{AB}}$.

---

Also gine auch so meine Begründung?

Ja, und sie ist sogar besser.
Es kommt nämlich überhaupt nicht darauf an, ob bei C ein rechter Winkel ist oder ob M der Mittelpunkt von AB ist, der Winkel zwischen den Winkelhalbierenden ist immer 90°.

---

Gute , ist damit fertig

Answer 2

Der Winkel ist 90°. Gib an welche Winkel bei M gleich groß sind.