Beweis für Tiefpunkt

Question

Aufgabe:

Beweis folgende Aussage:

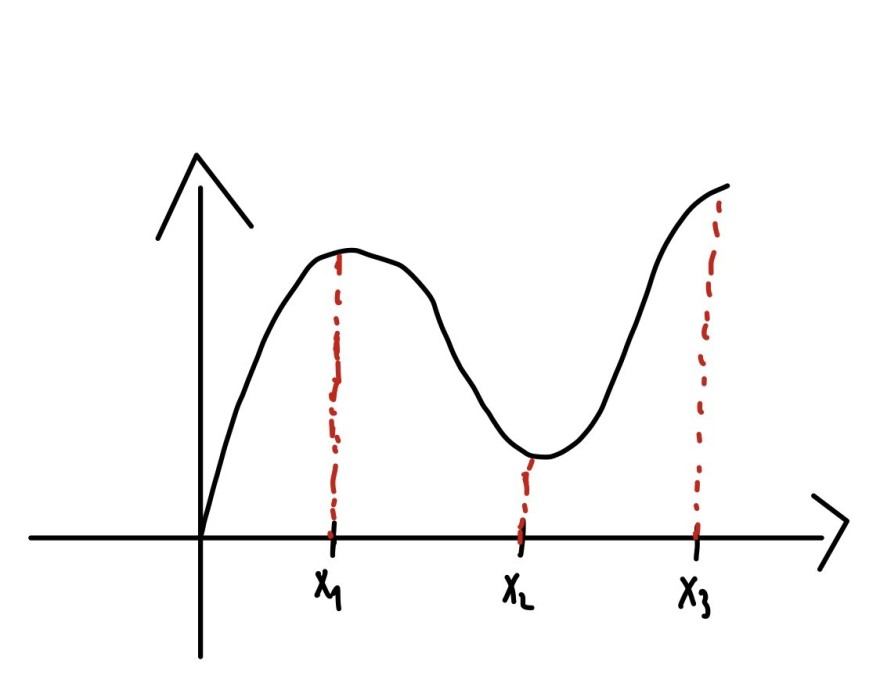
x1<x2<x3 mit f(x1) > f(x2) <f(x3), dann ∃ x ∈ R mit f′′(x)>0

Problem/Ansatz:

Ich habe mal versucht die ganze Geschichte zu skizzieren und kam auf folgendes ergebnis ( siehe Bild unten ). Dennoch fehlt mir die Idee wie ich das Beweisen könnte. Mir ist klar das die Funktion 2. mal ableitbar ist. Aber wie kann ich das beweisen das es auch ein TP gibt, da stehe ich auf dem Schlauch ich hoffe ihr könnt mir weiter helfen

Text erkannt:

\( m \)

Answer 1

Hallo

 1. muss man voraussetzen dass f 2 mal stetig differenzierter ist- 2. dann muss zwischen x1 und x2 irgendwo f(x) fallen. also f'<0 entsprechend f'>0 irgendwo zwischen x2 und x3  f' ist stetig, also muss es a) eine Nullstelle haben, b) da f# von negativ zu positiv geht muss f''>0

lul