Wie löse ich es richtig

Question

Aufgabe

Es sollen \( x_{1} \) Einheiten eines Produktes nach Verfahren \( 1, x_{2} \) Einheiten nach Verfahren 2 hergestellt werden. Unter den Nebenbedingungen
\( \begin{array}{r} 5 x_{1}+x_{2} \leq 17 \\ 5 x_{2} \leq 9 \\ 3 x_{1}+4 x_{2} \leq 13 \end{array} \)
und den Vorzeichenbedingungen \( x_{1}, x_{2} \geq 0 \) soll die Gesamtproduktion \( z=x_{1}+x_{2} \mathrm{maximal} \) werden. Verwenden sie dazu Excel-Solver.
Optimale Lösung: \( x_{1}=3,2 \quad x_{2}=0,8 \) Da man nicht 0,8 Einheiten eines Produktes herstellen kann müsste man hier auf oder abrunden.

Comments

Verwenden sie dazu Excel-Solver.

das weiß ich nicht, wie das geht. Wenn man es sich aufzeichnet ist die Lösung relativ klar:

https://www.desmos.com/calculator/vmrb8ao3fn

Die optimale ganzzahlige Lösung liegt bei \((3,\,1)\). Der Gitterpunkt liegt im grünen Bereich und am nächsten an der gestrichelten roten Geraden.

---

Und was ist Dein Problem bei dieser Veranstaltung?

---

Ich brauche eine Schritt für Schritt Erklärung wie es Schritt für Schritt per excel solver geht

---

Ich benutze den Wolfram-Solver

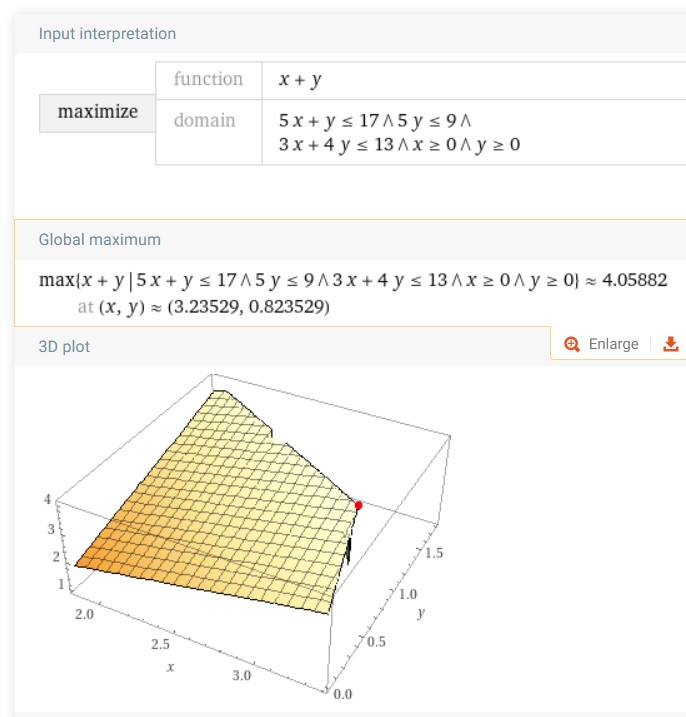
Da unklar ist, was eine Einheit ist, weißt du nicht, ob du nicht auch Teilmengen einer Einheit herstellen kannst.

Wenn die Einheit Stück ist dann kannst du keine Teilmenge herstellen. Wäre aber eine Einheit 1000 kg, dann könntest du auch eine Teilmenge davon Produzieren. Also würde ich einfach auf eine geeignete Anzahl nachkommastellen Runden.