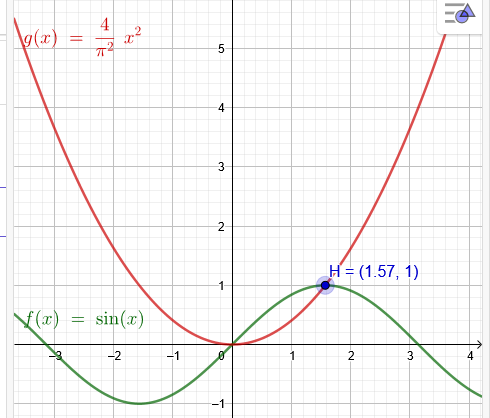
Eine zur Y-Achse achsensymmetrische Parabel läuft durch den ersten Hochpunkt der Sinusfunktion Rechts des Ursprungs. Sie umschließt mit dieser eine Fläche A. Welche Fläche besitzt A?
1.Hochpunkt der Sinusfunktion H(\( \frac{π}{2} \)|1)
f(x)=a*x^2
f(\( \frac{π}{2} \))=a*\( \frac{π^2}{4} \)
\( \frac{π^2}{4} \)*a=1 a=\( \frac{4}{π^2} \)
f(x)=\( \frac{4}{π^2} \)*\( x^{2} \)
\( A=\int \limits_{0}^{\frac{\pi}{2}}\left(\sin (x)-\frac{4}{\pi^{2}} \cdot x^{2}\right) \cdot d x=\left[-\cos (x)-\frac{4}{3 \pi^{2}} \cdot x^{3}\right]_{0}^{\frac{\pi}{2}}= \)
\( =\left[-\cos \left(\frac{\pi}{2}\right)-\frac{4}{3 \pi^{2}} \cdot\left(\frac{\pi}{2}\right)^{3}\right]-\left[-\cos (0)-\frac{4}{3 \pi^{2}} \cdot 0^{3}\right]=1-\frac{\pi}{6} \)