... befindet sich im Punkt A(-100|150). Sein Kurs wird durch (200|-100) gegeben ...
hast Du mal eine Skizze gemacht?
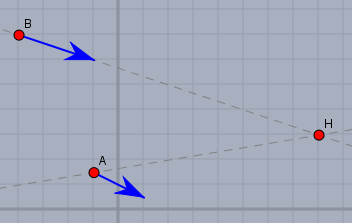
Zeigen Sie, dass beide sich auf richtigem Kurs zum Anlegepunkt H befinden.
So wohl eher nicht!
Der Rechenweg besteht darin, die Geraden aufzustellen, die den Weg der Jollen beschreiben.$$A:\quad \vec x = \begin{pmatrix} -100\\ 150\end{pmatrix} + \frac{t}{1\,\text{min}}\begin{pmatrix} 200\\ -100\end{pmatrix} \\ B: \quad \vec x = \begin{pmatrix} -400\\ 700\end{pmatrix} + \frac{t}{2\,\text{min}}\begin{pmatrix} -100 -(-400)\\ 600 -700\end{pmatrix}$$Zu beachten ist, dass bei Jolle A bereits die Fahrtrichtung (pro Minute) gegeben ist und bei Jolle B die Position, wo B in 2min sein wird. Um die Richtung zu bestimmen, ist der alte Standort abzuziehen.
Um festzustellen ob H erreicht werden kann, muss es jeweils eine Lösung für diese Gleichung geben$$H = \vec p + t \vec d$$wobei für \(\vec p\) und \(\vec d\) die Vektoren aus den Geradengleichungen einzugeben sind. Bei B gibt es so eine Lösung bei \(t=8\,\text{min}\). Bei A gibt es keine(!) Lösung, die beide Koordinaten erfüllt.
Gruß Werner