Aufgabe:

Text erkannt:
Aufgabe 2 (Polvnomfunktion, Differenzial- Integralrechnung) \( (7+7+10=24 \) Punkte)
a) Bestimmen Sie die ganzrationale Funktion vierten Grades, deren Graph achsensymmetrisch zur \( y- \) Achse ist.
Er hat im Punkt \( P(2 \mid-2) \) die Steigung 2 und einen Wendepunkt bei \( x=-1 \).
b) Ermitteln Sie die Schnittpunkte des Graphen der Funktion \( f \) mit der \( x \)-Achse sowie die Extrempunkte und die Wendepunkte von \( f \).
c) Eine Gerade \( g \) verläuft durch die Wendepunkte des Graphen der Funktion \( f \). Geben Sie eine geeignete Funktionsgleichung für die Funktion \( g(x) \) an. Zeichnen Sie den Graphen der Funktion \( f(x) \) und \( g(x) \) in einem gemeinsamen Koordinatensystem.
Die beiden Graphen schließen miteinander im Intervall \( -1 \leq x \leq 1 \) eine Fläche ein. Berechnen Sie den Flächeninhalt \( A \) dieser eingeschlossenen Fläche.
\( \underline{\text { Bearbeitungshinweis: }} \)
Die Ergebnisse sind ungerundet anzugeben.
Text erkannt:
Aufgabe 3 (Extremwertaufgabe) (13 Punkte)
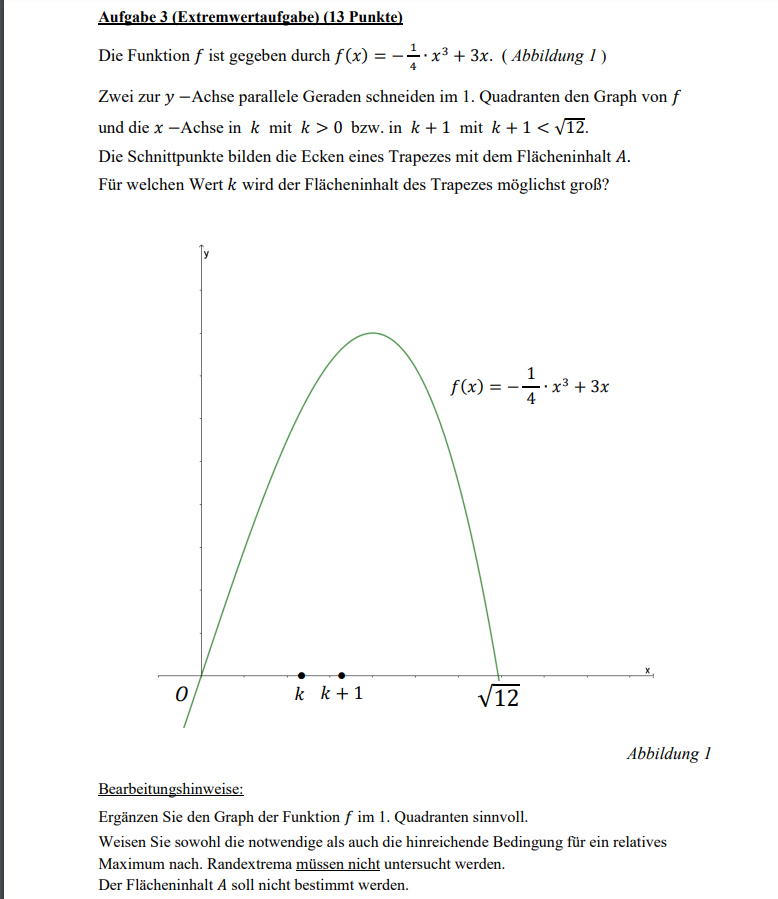
Die Funktion \( f \) ist gegeben durch \( f(x)=-\frac{1}{4} \cdot x^{3}+3 x \). (Abbildung 1 )
Zwei zur \( y \)-Achse parallele Geraden schneiden im 1. Quadranten den Graph von \( f \) und die \( x- \) Achse in \( k \) mit \( k>0 \) bzw. in \( k+1 \) mit \( k+1<\sqrt{12} \).
Die Schnittpunkte bilden die Ecken eines Trapezes mit dem Flächeninhalt \( A \).
Für welchen Wert \( k \) wird der Flächeninhalt des Trapezes möglichst groß?
Abbildung 1
\( \underline{\text { Bearbeitungshinweise: }} \)
Ergänzen Sie den Graph der Funktion \( f \) im 1. Quadranten sinnvoll.
Weisen Sie sowohl die notwendige als auch die hinreichende Bedingung für ein relatives
Maximum nach. Randextrema müssen nicht untersucht werden.
Der Flächeninhalt \( A \) soll nicht bestimmt werden.

Text erkannt:
Aufgabe 5 (Vektorielle Geometrie) \( (7+6=13 \) Punkte \( ) \)
Gegeben sind die Geraden
\( \mathrm{g}: \vec{r}(s)=\left(\begin{array}{l}0 \\ 2 \\ 1\end{array}\right)+s \cdot\left(\begin{array}{r}2 \\ 1 \\ -2\end{array}\right) \quad \) mit \( s \in \mathbb{R} \)
\( \mathrm{h}: \vec{r}(t)=\left(\begin{array}{c}0 \\ 7 \\ 1,5\end{array}\right)+t \cdot\left(\begin{array}{c}0 \\ b \\ \frac{b}{2}\end{array}\right) \) mit \( t \in \mathbb{R} \) und \( b \in \mathbb{R} \backslash\{0\} \)
und der Punkt \( P_{a}(2|a| 1) \).
a) Bestimmen Sie den reellen Parameter \( a \in \mathbb{R} \) so, dass der Punkt \( P_{a} \) den Abstand \( \frac{\sqrt{20}}{3} L E \) zur Geraden \( g \) hat.
b) Die Gerade \( h \) schneidet die \( z- \) Achse in einem Punkt \( A \). Bestimmen Sie die Koordinaten des Punktes \( A \).
Aufgabe 6 (Determinante) (6 Punkte)
Bestimmen Sie die Determinante der Matrix \( A \) in Abhängigkeit von \( a \in \mathbb{R} \).
\( A=\left(\begin{array}{rcc} -1 & 4 & 7 \\ 2 & a & 8 \\ 3 & 6 & a-4 \end{array}\right) \)
Ermitteln Sie den reellen Parameter \( a \in \mathbb{R} \), sodass die Gleichung \( \operatorname{det} A=360 \) erfüllt ist.
Problem/Ansatz:
So hier mein richtiger Versuch!
Vielleicht kann ja jemand diese Aufgaben bei Lust und Laune lösen. Bei mir geht es um Bestehen oder nicht Bestehen was diese Aufgaben betrifft.
Bei der 2 habe ich als Funktion: \( \frac{1}{4} \) \( x^{4} \) - \( \frac{3}{2} \) \( x^{2} \)
Als Flächeninhalt habe ich: \( \frac{8}{5} \)FE
Bei der 3 komme ich auf k=2. Mit dem Ansatz dass man bei der Trapezformel für a einmal f(k) und für b einmal f(k+1) benutzt sowie für die Höhe: 1 wegen (k+1 - k)
Bei der Vektoren habe ich gefühlt nur Mist raus da wäre ich mal gespannt...
Bei der Determinante kam ich auf zwei a Werte. Einmal 20 und einmal 5 glaube ich.
Da war auch noch eine Betragsgleichung wo ich 4 Fälle angesetzt habe, es aber nur 2 Fälle gab... Meint ihr da gibt es überhaupt Punkte für? Die hatte 10 Punkte...
Bin grad echt am Ende mit den Nerven