Hallo ich muss die folgende Aufgabe lösen:
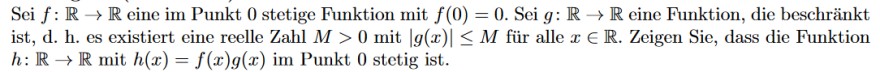
Text erkannt:
Sei \( f: \mathbb{R} \rightarrow \mathbb{R} \) eine im Punkt 0 stetige Funktion mit \( f(0)=0 . \) Sei \( g: \mathbb{R} \rightarrow \mathbb{R} \) eine Funktion, die beschränkt ist, d. h. es existiert eine reelle Zahl \( M>0 \) mit \( |g(x)| \leq M \) für alle \( x \in \mathbb{R} \). Zeigen Sie, dass die Funktion \( h: \mathbb{R} \rightarrow \mathbb{R} \) mit \( h(x)=f(x) g(x) \) im Punkt 0 stetig ist.
Meine Idee wäre es, dass hier nur gezeigt werden muss das g(x) stetig ist. Da bereits bekannt ist das f(x) stetig ist und die Multiplikation zweier steteiger Funktion ebenfalls stetig ist.
Mein Problem ist jetzt wie ich die Beschränktheit von g nutzen kann, um Stetigkeit zu zeigen.