Du kannst Deine Aufgabe mal hier
https://www.geogebra.org/m/jybmgrce
einbringen.
Weil ggb die Daten nicht rundungsfehlerfrei ins CAS birngt müsstest Du die Zeile
(5) C:={3 / 2, 3 / 2, -3 / 4, -1, 1/sqrt(2), 1/sqrt(2)}
händisch mit den Wurzeln überschreiben um exakte Ergebnisse zu erhalten
es wird gedreht mit
\(\small S \, := \, \left(\begin{array}{rr}\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\\end{array}\right)\)
auf \(q_D: \, x^{2} + 2 \; y^{2} + 2 \; x = \frac{3}{4}\)
und verschoben mit \(T \, := \, \left\{ x = x - \frac{1}{2}, y = y, \frac{-1}{4} \right\} \)
zu \(q_N: \, x^{2} + 2 \; y^{2} = 1\)
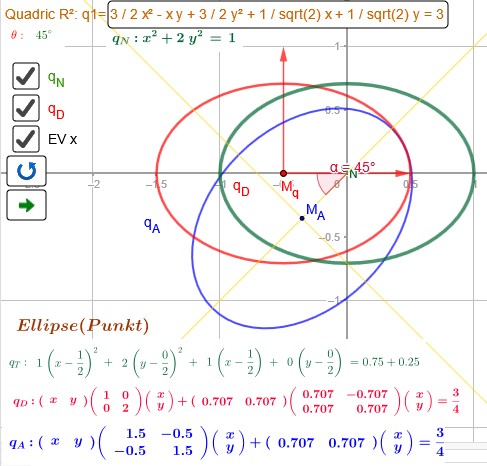
Du kannst nach die Ev vertauschen [EV x] um auf andere Lösungen zu kommen.