Hallo,
hast Du das schon mal gezeichnet?
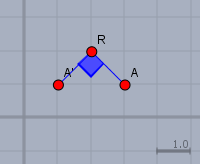
Offensichtlich ist der gedrehte Punkt \(A'=(1;\,1)\).
Soll das mit Matrizen gelöst werden? Kennst Du homogene Koordinaten? Was ist gerade das Thema bei Deiner Schule/Studium/Ausbildung?
Der 'Dienstweg' mit homogen Koodinaten sähe so aus. Man benötigt eine Transformation in ein System, wo \(R\) der Ursprung ist. Das Koordinatensystem in \(R\) ist$${}^0T_R = \begin{pmatrix}\underline 1& \vec p_R\\ \vec 0^T& 1\end{pmatrix}= \begin{pmatrix}1& 0& 2\\ 0& 1& 2\\ 0& 0& 1\end{pmatrix}$$Eine Drehung um 90° mit(!) dem Urzeigersinn ist eine negative Drehung also eine Drehung um -90°$$D_{-90°} = \begin{pmatrix}\cos(-90°)& -\sin(-90°)& 0\\ \sin(-90°)& \cos(-90°)& 0\\ 0& 0& 1\end{pmatrix}=\begin{pmatrix}0& 1& 0\\ -1& 0& 0\\ 0& 0& 1\end{pmatrix}$$zunächst wird \(A\) in das R-System transformiert$${}^RA = {}^RT_0 \cdot A = \left({}^0T_R\right)^{-1}\cdot A$$dann wird \({}^RA\) dort gedreht $${}^RA_{-90°} = D_{-90°} \cdot {}^RA = D_{-90°} \cdot\left({}^0T_R\right)^{-1}\cdot A$$ und wieder ins 0-System (Standard-System) zurück transformiert$$A' = {}^0T_R \cdot {}^RA_{-90°} = \underbrace{{}^0T_R \cdot D_{-90°} \cdot\left({}^0T_R\right)^{-1}}_{=\begin{pmatrix}0& 1& 0\\ -1& 0& 4\\ 0& 0& 1\end{pmatrix}}\cdot A$$In Zahlen gegossen:$$A'=\begin{pmatrix}0& 1& 0\\ -1& 0& 4\\ 0& 0& 1\end{pmatrix} \cdot \begin{pmatrix}3\\ 1\\ 1\end{pmatrix} = \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}$$
Gruß Werner