Aufgabe:
Bei einer Erhebung der Körpergröße von Studierenden wurden folgende Ergebnisse
beobachtet:
180, 179, 181, 178, 180, 182
Berechnen Sie die Kurtosis der Verteilung.
Problem/Ansatz:
Ich habe versucht, die Kurtosis über folgende Formel zu berechnen (siehe Bild):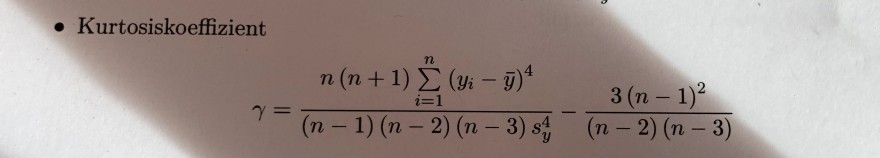
Text erkannt:
- Kurtosiskoeffizient
\( \gamma=\frac{n(n+1) \sum \limits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{4}}{(n-1)(n-2)(n-3) s_{y}^{4}}-\frac{3(n-1)^{2}}{(n-2)(n-3)} \)
Der Mittelwert, den ich ausgerechnet habe ist y=180 cm.
Varianz: s2y = 2 und Standardabweichung √2.
Nun bekomme ich aber bei jeder Rechnung eine andere Lösung raus. Ich habe alles versucht und dennoch bekomme ich die Lösung γ = −0.3 nicht raus.
Kann mir bitte jemand helfen?
Vielen Dank im Voraus