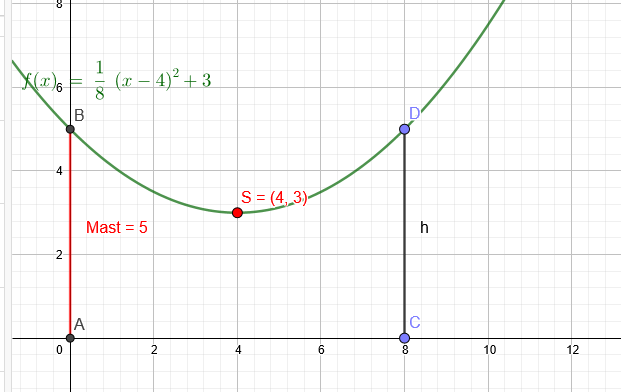
"Eine Wimpelkette wird an zwei hohen Pfählen in 5 m Höhe aufgehängt, deren Abstand 8 m beträgt. Am tiefsten Punkt hängt die Kette 3 m über dem Erdboden. Der Verlauf der Kette lässt sich annähernd durch den Graphen einer quadratischen Funktion f beschreiben. Ermitteln Sie eine Gleichung für eine solche Funktion f."
Ich verschiebe den Graph um 3 Einheiten nach unten und mache weiter mit der Nullstellenform der quadratischen Parabel:
p(x)=a*(x-\( \frac{1}{2} \)*8)^2
p(0)=a*(0-4)^2=16a 16a= 5-3=2 a=\( \frac{1}{8} \)
p(x)=\( \frac{1}{8} \)*(x-4)^2
f(x)=\( \frac{1}{8} \)*(x-4)^2+3