Quadratische Gleichungen, Parabel mit y = x^2 -10x + q geht durch den Punkt P(2/5).

Question

Eine nach oben geöffnete verschobene Normalparabel p₁ mit der Gleichung y = x² -10x + q geht durch den Punkt  P (2/5).

a) Berechne die Koordinaten der Schnittpunkte mit der x-Achse.

b) Die Gerade g schneidet die Achsen in Q (0/3) und R (3/0). Bestimme die Funktionsgleichung der Gerade und zeichne die Parabel sowie die Gerade in ein Koordinatensystem.

c) Berechne die Koordinaten der Schnittpunkte von Parabel p₁ und Gerade g.

d) Der Scheitel der Parabel p₁ wird um sieben Einheiten nach links und um drei Einheiten nach oben verschoben. Dadurch entsteht die Parabel p_2. Berechne nun die Schnittpunkte von g und p₂.

Answer 1

Eine nach oben geöffnete verschobene Normalparabel p₁ mit der Gleichung y = x² -10x + q geht durch den Punkt  P (2/5).

y = x² - 10·x + 21         |vgl. Antwort von Mathecoach

a) Berechne die Koordinaten der Schnittpunkte mit der x-Achse.

y = x² - 10·x + 21 = 0           |quadratische Gleichung: Formel oder direkt faktorisieren

(x-7)(x-3) = 0

x1 = 7, x2 = 3 sind die Nullstellen

b) Die Gerade g schneidet die Achsen in Q (0/3) und R (3/0). Bestimme die Funktionsgleichung der Gerade und zeichne die Parabel sowie die Gerade in ein Koordinatensystem.

Ansatz für g: y = mx + q         |y-Achsenabschnitt q = 3 wegen Q(0|3)

Wenn du die beiden Punkte und die Gerade einzeichnest, siehst du sofort, dass die Steigung m=  -3/3 = -1/1 = -1 ist. 

Daher g:  y = -x + 3

c) Berechne die Koordinaten der Schnittpunkte von Parabel p₁ und Gerade g.

Funktionsgleichungen gleichsetzen:

-x + 3 = x² - 10·x + 21            

0 = x^2 - 9x + 18           |Wieder eine quadratische Gleichung. Formel oder faktorisieren.

0=(x-3)(x-6)

x1 = 3

x2 = 6           die beiden Schnittstellen

Schnittpunkte: x1 und x2 noch in eine der Funktionsgleichungen einsetzen

y = -x + 3

y1 = - 3 + 3 = 0          S1(3, 0)
y2 = -6 + 3 = -3           S2(6, -3)

d) Der Scheitel der Parabel p₁ wird um sieben Einheiten nach links und um drei Einheiten nach oben verschoben. Dadurch entsteht die Parabel p_2. Berechne nun die Schnittpunkte von g und p₂.

Beachte: Da wird gleich die ganze Parabel p1 um sieben Einheiten nach links und um drei Einheiten nach oben verschoben.

um sieben Einheiten nach links verschieben: x durch x+7 ersetzen

und um drei Einheiten nach oben verschoben: y durch y-3 ersetzen. Oder äquivalent dazu in der Funktionsgleichung rechts 3 addieren.

p1: y = x² - 10·x + 21

p2: y -3 =  (x+7)² - 10·(x+7) + 21         |+3

y =x^2 + 14x + 49 - 10x - 70 + 24

y = x^2 + 4x + 3

nun schneiden mit g

x^2 + 4x + 3 = -x + 3

x^2 + 5x = 0              |quadratische Gleichung: faktorisieren
x(x+5) = 0

x1 = 0, x2 = -5

Schnittpunkte:

g: y = -x + 3

-0 + 3 = 3 ---> S1(0,3)

-(-5) + 3 = 8 ---> S2(-5, 8)

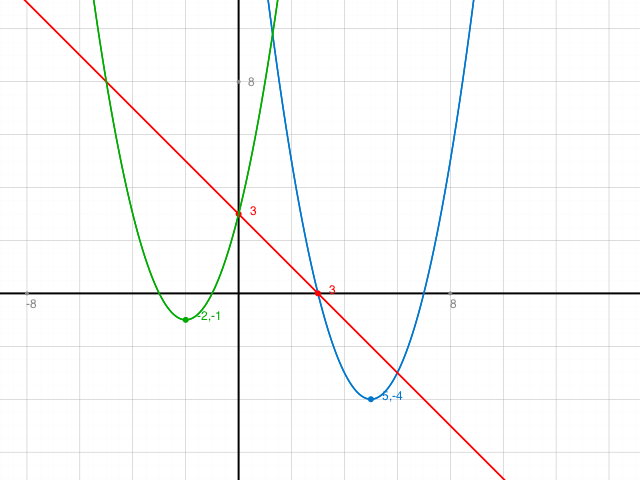
Kontrolle: Graph:

Ergänze noch die Beschriftung der Achsen, die Klammern um die Scheitelpunktskoordinaten. Die Schnittpunkte kannst du auch noch alle beschriften.

Answer 2

Eine nach oben geöffnete verschobene Normalparabel p₁ mit der Gleichung y = x² -10x + q geht durch den Punkt  P (2/5).

Wir setzen den Punkt in die Funktionsgleichung ein:

y = x^2 - 10·x + q
5 = 2^2 - 10·2 + q
q = 21

Damit lautet die Funktionsgleichung

y = x^2 - 10·x + 21

Kommst du dann alleine weiter?

Comments

Weitere Hilfe wäre gut, da ich bis jetzt kaum Parabeln und deren Punkte, etc. berechnet habe.