Hallo,
In der Lösung steht nur 71,57°.
Geht das mit dem Taschenrechner oder mit Additionstheoremen ?
das geht mit Nachdenken und der Kenntniss, was der Sinus ist. Und dann im Kopf!
Die zu lösende Gleichung ist doch$$96 = 96 \cdot \frac{\sin(\varphi)}{\sin\left(\varphi + 36,87°\right)}$$und nun sollte schon mal in's Auge fallen, dass die Gleichung genau dann erfüllt ist, wenn der Bruch den Wert \(1\) annimmt, bzw. wenn Zähler und Nenner gleich sind. D.h.$$\sin(\varphi) = \sin\left(\varphi + 36,87°\right)$$und wenn man sich den Einheitskreis ansieht, wo man für einen bestimmten Winkel den Sinus ablesen kann, dann ist klar dass ... $$\varphi = 90°- \frac{36,87°}{2} = 90° - 18,435° = 71,565°$$.. sein muss (Vorausgesetzt: \(\varphi \gt 0\)). Wird diese Überlegung durch folgendes Bild klar?
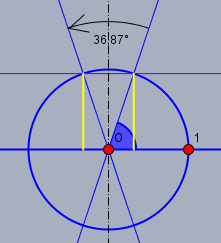
Die gelben Strecken sind der Sinus von \(\varphi\) (blau) und von \(\varphi + 36,87°\).
Gruß Werner