Aufgabe:
Rekursiv gegebene Zahlenfolge
Problem/Ansatz:
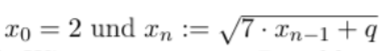 ,
,
Wie muss q gewählt werden, damit die Folge zum Grenzwert 17/2 konvergiert?
Meine Überlegung:
x2=7x+q ,wobei 2 eine Lösung ist.
Leider bin ich mir wirklich unsicher, was diese Aufgabe angeht.
Danke für alle Tipps!
Text erkannt:
\( x_{0}=2 \) und \( x_{n}:=\sqrt{7 \cdot x_{n-1}+q} \)