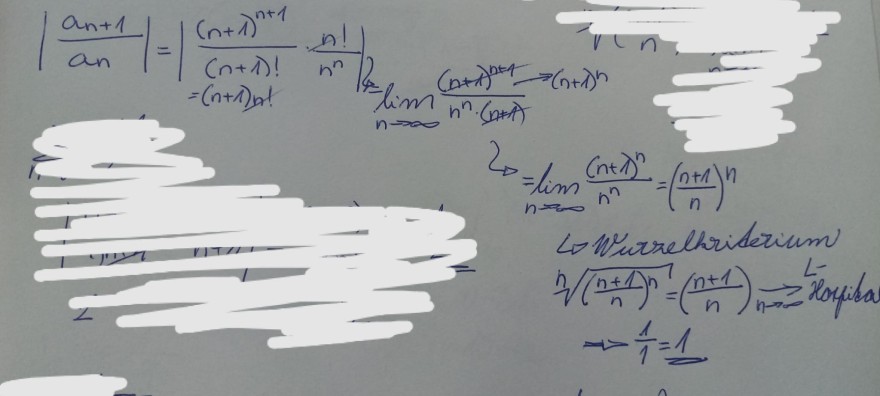Konvergez einer Reihe bestimmen

Question

Aufgabe:

Konvergz einer Reihe bestimmen - kann man mehrere Konvergenzkriterien verwenden?

Problem/Ansatz:

PROBLEM GEFUNDEN, danke :)

Konvergenz/Divergenz dieser Reihe soll bestimmt werden.

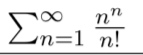
Text erkannt:

\( \sum \limits_{n=1}^{\infty} \frac{n^{n}}{n !} \)

Was ich gemacht habe: zuerst habe ich den Quotiententest angewendet- am Ende habe ich einen unbestimmten Ausdruck: (n+1)^n/(n^n) bekommen.... Deswegen habe ich diesen Ausdruck nochmal mit dem Wurzelkriterium geprüft - da habe ich am Ende (n+1)/n bekommen - L Hospital angewendet und 1 als den Grenzwert bekommen.

Diese Reihe soll aber divergieren.

Soll ich das so verstehen, dass man immer nur eines Kriterium anwenden darf?

Danke.

Answer 1

Aloha :)

Die Folge der Summanden \(a_n\coloneqq\frac{n^n}{n!}\) ist keine Nullfolge:$$a_n=\frac{n^n}{n!}=\frac{n}{1}\cdot\frac{n}{2}\cdot\frac{n}{3}\cdots\frac{n}{n}\ge1$$Damit ist ein notwendiges Kriterium für die Konvergenz der Summe verletzt.

Die Summe divergiert.