Flächeninhalt Figur im Einheitskreis durch Funktion

Question

Aufgabe

Problem/Ansatz

Man hat gezeigte Figur in der oberen hälfte des Einheitskreises. Jetzt soll man eine Funktion für den Flächeninhalt der Figur aufstellen bzw. erklären wie man auf folgende Funktion kommt:

f (α) = cos(α) + sin(α) cos(α)

Answer 1

Die untere Teilfläche ist ein Rechteck der Breite 2*cos α und der Höhe sin α.

Die dreieckige obere Teilfläche hat die Breite 2*cos α und die Höhe (1-sin α).

Comments

Die Hälfte der Figur ist ein Trapez mit den parallelen Seiten 1 und sin α sowie der Höhe cos α

---

Danke! Wie genau komme ich auf diese Werte? Bzw. unter welchem Namen kann ich eine Erklärung bzw. Herleitung dazu finden?

---

Okay bin einfach nur dumm. Trotzdem danke :)

---

Bzw. unter welchem Namen kann ich eine Erklärung bzw. Herleitung dazu finden?

... komisches Ansinnen? Selber denken macht schlau ;-)

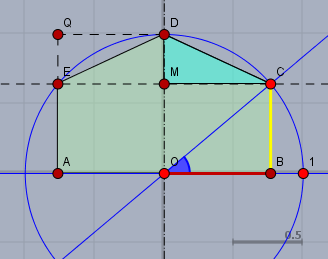
Schneide das Dreieck $MCD$ (blau) aus der Figur heraus und klebe es in die Position von $\triangle DQE$. Dann bleibt links das Rechteck $AODQ$ stehen mit den Abmessungen$$F_1 = \cos(\alpha) \cdot 1$$und rechts das Rechteck $OBCM$ mit den Abmessungen $$F_2= \cos(\alpha) \cdot \sin(\alpha)$$Die Gesamtfläche der Figur ist die Summe von beiden.

Du musst dazu wissen, dass die rote Strecke der Cosinus und die gelbe der Sinus des Winkels $\alpha$ (blau) ist. Und die Flächenformel für das Rechteck findest Du hier.