Tangenssatz aus Mollweide

Question

Aufgabe:

Herleitung des Tangenssatzes aus den Mollweide-Gleichungen

Problem/Ansatz:

Der Tangenssatz wird in meiner Vorlage hergeleitet aus der Division der beiden Mollweide-Gleichungen für (a+b)/c und (a-b)/c. Ich mache den ersten Schritt von (1) nach (2) mit der Multiplikation der einen Gleichung mit dem Kehrwert der anderen. Doch die Schritte (3), (4) und (5) in der Vorlage kann ich nicht nachvollziehen und bitte um Hilfe!

\( (1) \frac{\frac{\sin \frac{2-\beta}{2}}{\sin 90^{\circ}+\frac{8}{2}} \leqslant \frac{a}{b}}{\frac{\sin 2-p-\frac{c}{6}}{\frac{6}{6}}} \)

(2) \( \frac{\sin \frac{2-\beta}{2} \cdot \cos \frac{\gamma}{2}}{\sin \left(90^{\circ}+\frac{r}{2}\right) \cdot \sin \frac{2-8}{2}} \)
(3) \( \frac{\frac{\cos 2-\beta}{2} \cdot \cos \frac{\pi}{2}}{\sin \frac{1}{2} \cdot \frac{\sin 2-\beta}{2}} \)
\( (4) \frac{\cot \frac{\gamma}{2}}{\tan \frac{2-p}{2}} \)
\( \left.(5) \quad \frac{\tan (2+\beta)}{2}\right) \)
\( \tan \frac{2-\beta}{2} \)

Comments

Kannst du  bitte deine Formeln verbessern, so sind sie für mich nicht lesbar, etwa sin((2-β)/2) oder sin90°+8/2 ??

lul

---

Mein Problem ist, dass ich einen Text in Handschrift hochgeladen habe, der auch in der Vorschau korrekt sichtbar war. Dann aber hat das Programm offensichtlich automatisch die Handschrift in Drucktext umgewandelt, mit schlimmen Fehlern. Kopiere ich diesen nun hierher, kann ich ihn selbst kaum lesen und korrigieren. Was tun?

\((1) \frac{\frac{\sin \frac{alpha-\beta}{2}}{\sin 90^{\circ}+\frac{8}{2}} \leqslant \frac{a}{b}}{\frac{\sin 2-p-\frac{c}{6}}{\frac{6}{6}}} \)(2) \( \frac{\sin \frac{2-\beta}{2} \cdot \cos \frac{\gamma}{2}}{\sin \left(90^{\circ}+\frac{r}{2}\right) \cdot \sin \frac{2-8}{2}} \)(3) \( \frac{\frac{\cos 2-\beta}{2} \cdot \cos \frac{\pi}{2}}{\sin \frac{1}{2} \cdot \frac{\sin 2-\beta}{2}} \)\( (4) \frac{\cot \frac{\gamma}{2}}{\tan \frac{2-p}{2}} \)\( \left.(5) \quad \frac{\tan (2+\beta)}{2}\right) \)\( \tan \frac{2-\beta}{2} \)

---

Es gibt im Latex das \LARGE Statement.

---

Damit weiß ich leider nichts anzufangen...

---

Ohne und mit \LARGE:

\( (1) \frac{\frac{\sin \frac{2-\beta}{2}}{\sin 90^{\circ}+\frac{8}{2}} \leqslant \frac{a}{b}}{\frac{\sin 2-p-\frac{c}{6}}{\frac{6}{6}}} \)

\( (1) \LARGE \frac{\frac{\sin \frac{2-\beta}{2}}{\sin 90^{\circ}+\frac{8}{2}} \leqslant \frac{a}{b}}{\frac{\sin 2-p-\frac{c}{6}}{\frac{6}{6}}} \)

---

Das sieht viel besser aus. Doch wie kann ich die Fehler (statt alpha und gamma steht jeweils 2) herauskorrigieren?

---

Ok, ich werde Mollweide etc. erstmal drangeben und versuchen, Latex zu lernen. Oder kann man das MatheLounge-Programm daran hindern, eine handschriftliche Rechnung in Drucktext  umzuwandeln?

---

Inzwischen habe ich das Problem zum Teil selbst lösen können. Es geht um die Herleitung des Tangenssatzes aus der Division der beiden Mollweide-Gleichungen (a+b)/c und (a-b)/c durcheinander. Nur der letzte Schritt zum Tangenssatz bereitet mir noch Kopfzerbrechen.

(1) (cot (gamma/2))/(tan((alpha - beta)/2)) =

(2) = ((tan (alpha + beta)/2))/(tan (alpha - beta)/2))

Wie wird  cot (gamma/2) in (1) zu (tan (alpha + beta)/2) in (2)?

Anders gewendet: Warum ist cot (gamma/2) gleich tan ((alpha + beta)/2)?

Es bleibt mir das Problem, dass eine hochgeladene handschriftliche Rechnung durch das MatheLounge-Programm automatisch in eine fehlerhafte Druckfassung umgewandelt wird. Wie kann ich sicherstellen, dass die handschriftliche Fassung im jpg-Format durch das Hochladen nicht verändert wird?

---

Eigentlich sollte auch das jpg-Bild noch sichtbar sein.

---

Inzwischen habe ich die Lösung selbst gefunden. Meine Frage war, warum ist cot gamma/2 = tan (alpha + beta)/2 :

(1) alpha + beta + gamma = 180°

(2) gamma = 180° − (alpha + beta)

(3) gamma/2 = 90° − ((alpha + beta)/2)

(4)(alpha + beta)/2  = (90° − gamma/2)

(5) tan ((alpha + beta)/2) = tan (90° − (gamma/2))

(6) Da Tangens und Kotangens im Verhältnis tan (90° − θ) = cot θ stehen:

(7) tan ((alpha + beta)/2) = cot (gamma/2) QED

Jetzt versuche ich meine handschriftliche Rechnung hier hochzuladen:

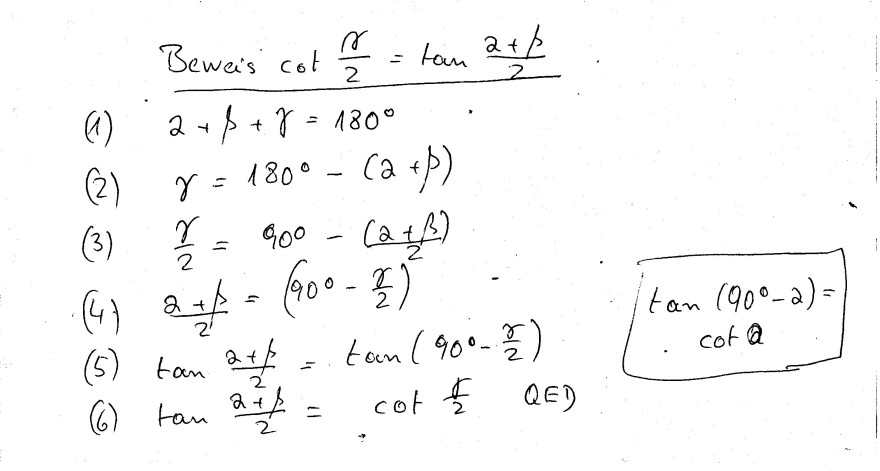
Text erkannt:

\( \frac{\text { Bewais } \cot \frac{\gamma}{2}=\tan \frac{2+\beta}{2}}{2+\beta+\gamma=180^{\circ}} \)
(1) \( 2+\beta+\gamma=180^{\circ} \) (2) \( \gamma=180^{\circ}-(2+\beta) \)
(3) \( \frac{\gamma}{2}=90^{\circ}-\frac{(\alpha+\beta)}{2} \)
(4) \( \frac{2+1}{2}=\left(90^{\circ}-\frac{\gamma}{2}\right)^{2} \).
(5) \( \tan \frac{2+f}{2}=\tan \left(90^{\circ}-\frac{\gamma}{2}\right) \)
\( \tan \left(90^{\circ}-2\right) \) \( \cot a \)
(6) \( \tan \frac{2^{2}+\beta}{2}=\cot \frac{\gamma}{2} \quad Q E D \)

In der Vorschau sehe ich sie jetzt noch als Handschrift. Nun sende ich den ganzen Kommentar mit der handschriftlichen Version und sehe tatsächlich beide Versionen vor mir, wie Gast azu0815 annahm. Yippie! Allerdings ist die umgewandelte Version fehlerhaft und deshalb zu ignorieren!