Lineare Algebra Wählerwanderungen

Question

Aufgabe:

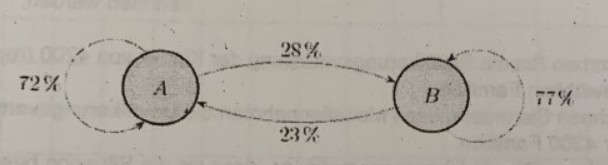
Das Übergangsdiagramm erfasst die Wählerwanderungen zwischen den Parteien A und B innerhalb eines Jahres. Zum jetzigen Zeitpunkt wählen \( 42 \% \) die Partei A und \( 58 \% \) die Partei B.

a) Ermitteln Sie, wie sich die Verteilung der Wähler auf diese beiden Parteien in den nächsten 3 Jahren entwickelt.

b) Welche Prognosen sind langfristig möglich unter der Voraussetzung, dass die Übergangsquoten konstant bleiben?

c) Bestimmen Sie die Verteilung der Wähler auf die beiden Parteien ein Jahr zuvor.

Problem/Ansatz:

Hallo,
habe ich Aufgabe a) und b) richtig bearbeitet? Wenn nicht würde ich mich freuen wenn mir jemand helfen könnte. Außerdem weiß ich leider nicht wie ich Aufgabe c) bearbeiten soll. Vielleicht mit dem Vorbestandvektor??? Aber wie wende ich es dann genau an?
Schonmal vielen Dank.

a) \( A \)                 B

\( A\left(\begin{array}{ll}0,72 & 0,23 \\ 0,28 & 0,77\end{array}\right) \cdot\left(\begin{array}{c}0,42 \\ 0,58\end{array}\right)=\left(\begin{array}{l}0,4358 \\ 0,5642\end{array}\right) \)
\( A\left(\begin{array}{cc}A & B \\ 0,72 & 0,23 \\ 0,28 & 0,77\end{array}\right) \cdot\left(\begin{array}{l}0,4358 \\ 0,5642\end{array}\right)=\left(\begin{array}{l}0,4435 \\ 0,5564\end{array}\right) \)
\( A\left(\begin{array}{cc}A & B \\ 0,72 & 0,23 \\ 0,28 & 0,77\end{array}\right) \cdot\left(\begin{array}{c}0,4435 \\ 0,5564\end{array}\right)=\left(\begin{array}{l}0,4472 \\ 0,5526\end{array}\right) \)
Nach drei Jahren sient die verteiluny wie Folft aus: bei \( A \), 4472 und bei \( B \) 0,5526 Wähler.

b)
\( \left(\begin{array}{ll} 0,72 & 0,23 \\ 0,28 & 0,77 \end{array}\right)^{2222}=\left(\begin{array}{ll} 0,4509 & 0,4509 \\ 0,549 & 0,549 \end{array}\right) \)

Die langfristige Prognose.

Answer 1

a)
v1 = [0.72, 0.23; 0.28, 0.77]·[0.42; 0.58] = [0.4358; 0.5642]
v2 = [0.72, 0.23; 0.28, 0.77]·[0.4358; 0.5642] = [0.443542; 0.556458]
v3 = [0.72, 0.23; 0.28, 0.77]·[0.443542; 0.556458] = [0.4473355799; 0.5526644199]

b)
[0.72, 0.23; 0.28, 0.77]·[x; y] = [x, y] → x = 23/51 ∧ y = 28/51

c)
[0.72, 0.23; 0.28, 0.77]·[x; y] = [0.42; 0.58] → x = 19/49 ∧ y = 30/49

Comments

Ich verstehe b) und c) nicht wie soll ich auf die Ergebnisse kommen?

---

Schreibe die Matritzengleichung als Lineares Gleichungssystem. Dieses löst du dann.

[0.72, 0.23; 0.28, 0.77]·[x; y] = [x, y]

0.72·x + 0.23·y = x
0.28·x + 0.77·y = y

Da dieses Gleichungssystem noch linear Abhängig ist, kannst du eine dre obigen Gleichungen durch

x + y = 1

ersetzen. Damit bekommst du dann mein Ergebnis und einen gültigen Verteilungsvektor heraus.

---

Vielen Dank!!