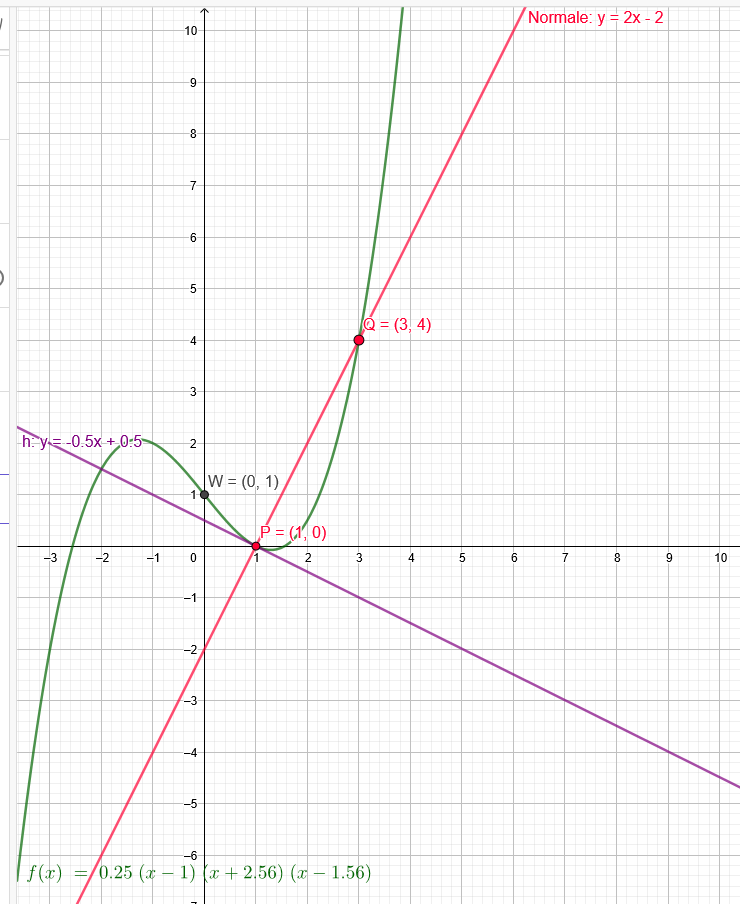
"Gesucht ist eine Parabel 3. Ordnung (y = a\( x^{3} \) + b\( x^{2} \) + cx + d). Der Wendepunkt ist auf der y-Achse (y-Wert unbekannt). Gegeben sind außerdem die Kurvennormale, die in P(1|0) und Q(3|4) die Parabel noch einmal schneidet."
Weg über die Nullstellenform der kubischen Parabel:
f(x)=a*(x-1)*(x-N₁)*(x-N₂)
f(3)=a*(3-1)*(3-N₁)*(3-N₂)
2a*(3-N₁)*(3-N₂)=4 → a*(3-N₁)*(3-N₂)=2 → a=\( \frac{2}{(3-N₁)*(3-N₂)} \)
f(x)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(x-1)*(x-N₁)*(x-N₂)]
f´(x)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(x-N₁)*(x-N₂)+(x-1)*(x-N₂)+(x-1)*(x-N₁)]
Steigung der Geraden (Kurvennormale) durch P(1|0) und Q(3|4):
m₁=\( \frac{4-0}{3-1} \)=2
Steigung der Tangente durch P(1|0) ist m=-0,5
f´(1)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(1-N₁)*(1-N₂)+(1-1)*(1-N₂)+(1-1)*(1-N₁)]
\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(1-N₁)*(1-N₂)]=-0,5
f´(x)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(x-N₁)*(x-N₂)+(x-1)*(x-N₂)+(x-1)*(x-N₁)]
f´´(x)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(x-N₂)+(x-N₁) +(x-N₂) +(x-1) +(x-N₁)+(x-1)]
"Wendepunkt auf y-Achse: f´´(0)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[(0-N₂)+(0-N₁) +(0-N₂) +(0-1) +(0-N₁)+(0-1)]
f´´(0)=\( \frac{2}{(3-N₁)*(3-N₂)} \)*[-2N₂-2N₁ -2]
f´´(0)=\( \frac{1}{(3-N₁)*(3-N₂)} \)*[-N₂-N₁ -1]
\( \frac{1}{(3-N₁)*(3-N₂)} \)*[-N₂-N₁ -1]=0 → -N₂-N₁ -1=0 → N₂=-N₁ -1
\( \frac{2}{(3-N₁)*(3-(-N₁ -1))} \)*[(1-N₁)*(1-(-N₁ -1))]=-0,5
\( \frac{2}{(3-N₁)*(4+N₁ ))} \)*[(1-N₁)*(2+N₁ ))]=-0,5
1.)N₁≈-2,56 2.) N₁≈1,56
1.)N₂≈1,56 2.)N₂=-2,56
a=\( \frac{2}{(3+2,56)*(3-1,56)} \)=\( \frac{2}{(5,56)*(1,44)} \)≈0,25
f(x)=0,25*(x-1)*(x+2,56)*(x-1,56)