Aloha :)
Ich habe mal die beiden Funktionen$$f(x)=5\left(e^{-0,3x}-e^{-4x}\right)\quad\text{und}\quad g(x)=2,8$$in ein Koordinatensystem geplottet.
~plot~ 5*(e^(-0,3x)-e^(-4x)) ; 2,8 ; [[0|4|0|4]] ~plot~
Wir erkennen zwei Schnittpunkte, einen bei \(x\approx0,25\), den anderen bei \(x\approx1,9\).
Eine geschlossene Lösung des Problems ist leider nicht möglich. Wir können aber die Funktion \(f(x)\) an einem Punkt \(x_0\) durch ihre Tangente annähern:$$t(x)\approx f(x_0)+f'(x_0)\cdot(x-x_0)$$Dann berechnen wir, bei welchem \(x\)-Wert diese Tangente den Funktionswert \(2,8\) hat:$$t(x)\stackrel!=2,8\implies$$$$f(x_0)+f'(x_0)\cdot(x-x_0)=2,8\implies$$$$x=x_0+\frac{2,8-f(x_0)}{f'(x_0)}$$Dieses \(x\) verwenden wir nun als neuen Näherungspunkt \(x_0\) und wiederholen die ganze Prozedur. Das gibt dann eine Rekursionsformel:$$x_{n+1}=x_n+\frac{2,8-f(x_n)}{f'(x_n)}=x_n+\frac{2,8-5\left(e^{-0,3x_n}-e^{-4x_n}\right)}{5\left(-0,3e^{-0,3x_n}+4e^{-4x_n}\right)}$$
Ich habe das mal in Excel eingegeben:
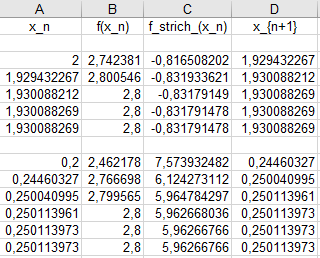
Wir finden mit dem Verfahren beide Schnittstellen:$$x_1=0,250113973\quad;\quad x_2=1,930088269$$