aber warum wenn ich in eine Kombination von 2 * 4 = 8 nehme, geht aber nicht 1260 ist NICHT durch 8 teilbar?

Question

aber warum wenn ich in eine Kombination von 2 * 4 = 8 nehme, geht aber nicht 1260 ist NICHT durch 8 teilbar?

3 Antworten

Beste Antwort

Hallo Zhari,$$1260 = 2\cdot 2\cdot 3\cdot 3 \cdot 5\cdot 7$$oben siehst Du die Primteiler der Zahl 1260. Primteiler sind die Teiler, die nicht mehr in ein anderes Produkt außer der $1$ und sich selbst zerlegt werden können.

Um eine neues Produkt zu bilden - z.B. $2\cdot 3 = 6$, so ist das Produkt - also die $6$ - genau dann auch ein Teiler von 1260, wenn Du von den Primteilern jeden Primteiler nur einmal entnommen hast. Also im Fall von $2\cdot 3$ bedeutet dies:$$1260 = {\color{red}2}\cdot 2\cdot {\color{red}3}\cdot 3 \cdot 5\cdot 7 \quad \quad {\color{red}2\cdot 3} = 6 \space \checkmark$$$6$ ist ein Teiler von 1260, da die Teiler der $6$ - also die 2 und die 3 - beide mindestens einmal in der 1260 vorkommen.

Bei $4\cdot 2$ ist das anders$$1260 = {\color{red}2}\cdot 2\cdot 3\cdot 3 \cdot 5\cdot 7 \quad \quad {\color{red}2} = 2\space \checkmark\\1260 = {\color{red}2\cdot 2}\cdot 3\cdot 3 \cdot 5\cdot 7 \quad \quad {\color{red}2\cdot 2} = 4\space \checkmark$$$2$ ist ok und $4$ ist ok, beide sind Teiler von 1260.

Aber $$1260 = {\color{red}2\cdot 2}\cdot 3\cdot 3 \cdot 5\cdot 7 \quad \quad \underbrace{{\color{red}2\cdot 2}}_{=4} \cdot 2 = 8\space ?$$Die 2 ist nur zweimal Primteiler von 1260. Also darf die 2 in dem Produkt auch nur maximal zweimal vorkommen. Die $8$ kann also kein Teiler von 1260 sein, weil hier eine 2 mehr benötigt wird, als in 1260 vorhanden ist.

Gruß Werner

Beantwortet 18 Mär 2022 von Werner-Salomon

Hallo Zahri,

Stell Dir die Zahl 1260 wie einen Obstkorb vor. Die Zahl 2 ist ein Apfel, die Zahl 3 eine Birne, die 5 eine Zitrone und die 7 eine Orange. Dann sind im Obstkorb
zwei Äpfel, für die (2)
zwei Birnen, für die (3)
eine Zitrone, für die (5)
eine Orange, für die (7) weil$$1260 = 2 \cdot 2 \cdot 3\cdot3\cdot 5\cdot 7$$
Um ein Produkt aus zwei Faktoren zu bilden kannst Du Dir nun zweimal eine bestimmte Menge von Obst aus dem Obstkorb heraus nehmen. Also für das Produkt $3\cdot 6 = 18$ nimmst Du Dir eine Birne (3) für die die $3$ und für die $6$ dann die zweite Birne(3) aus dem Korb und einen Apfel(2). Das macht $3\cdot 2=6$. Das ist möglich.
Für das Produkt $2\cdot4=8$ nimmst Du Dir einen Apfel(2) für die $2$ und für die $4$ bräuchtest Du jetzt noch zwei Äpfel(2). Es ist aber nur noch ein Apfel im Obstkorb vorhanden. Also für die $4$ ist nicht mehr genug Obst da. Folglich ist das Produkt $2\cdot 4$ kein Teiler von 1260.

aber 2* 4= 8 = 2 * 2 * 2= 8 → die 2 ist DREIMAL vorkommt, deswegen geht nicht 1260 /8? stimmt?

genau so ist es richtig.

Kommentiert 19 Mär 2022 von Werner-Salomon

Zitat"welche Frage meinst Du?"

Hier Werner: :

ich habe frühe diese Aufgabe gelöst aber nach viele Versuche. ich wollte NUR wissen wie kommt ich vom ersten Versuch zur richtigen Lösung:

Di Aufgabe lautet: Ein Gebäude ist 19,50 m lang und 8,40 breit. Von welchem Punkt sieht man beide 'Geäudeseiten unter einem Winkel von 30 °? Beschreibe dein Vorgang?

Hier meine Lösung:

hier ist Bild 1( keinen Schnittpunkt, also keine Lösung)

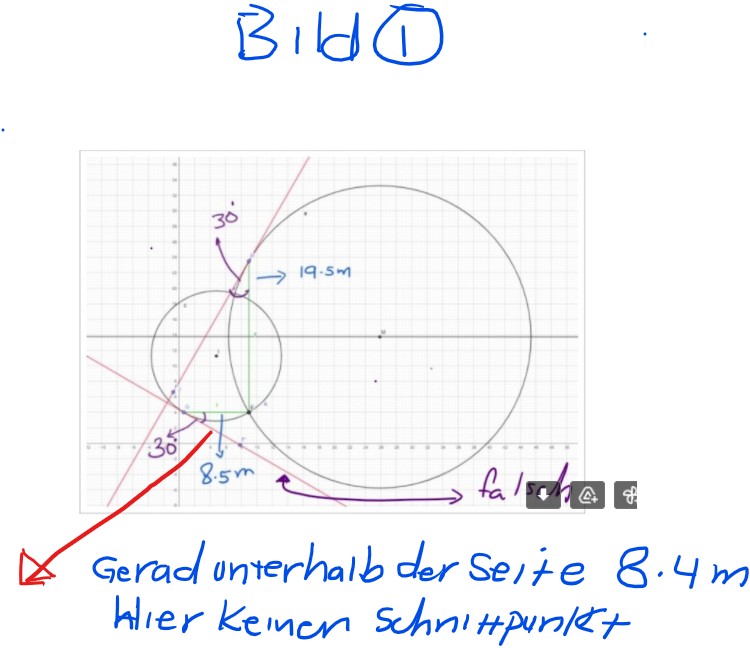
Text erkannt:

Bid(I)
Gerad unterhalb der Seste $ 8.4 \mathrm{~m} $ hier Keiner Schnittpunlkt

jetzt Bild 2( Ja es gibt einen Schnittpunkt, also eine Lösung--> beides Seiten unter 30 Grad zu sehen)

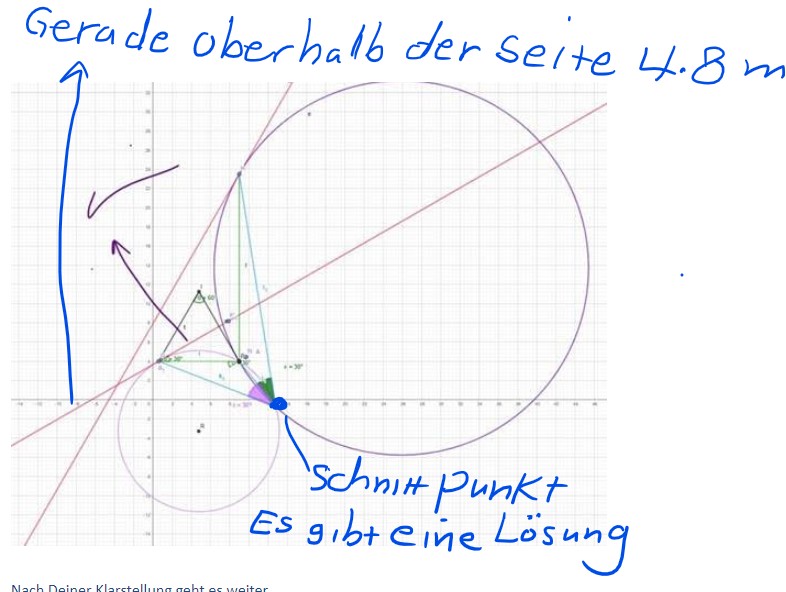
Text erkannt:

Gerade oberhalb der seite L.8 m
Es a ghte punkt
Es gibteine Losung

und meine Frage: warum bei BIld 1 keine Lösung ( keinen Schnittpunkt) aber bei Bild 2 , ja es gibt eine Lösung? Ich habe zuerst viel mal versucht bis ich auf Bild2 gekommen bin und die Lösung gefunden.
wie weiss ich schon ,dass ich die Gerade oberhalb Zeichnen und nicht unterhalb der Seite 8.4 m , damit die Lösung richtig rauskommt

Kommentiert 22 Mär 2022 von Zahri Ameer

Hallo Zahri,

wie weiss ich schon ,dass ich die Gerade oberhalb Zeichnen und nicht unterhalb der Seite 8.4 m , damit die Lösung richtig rauskommt

Die Aufgabe bestand doch darin, den Punkt zu finden, von dem man auf zwei Gebäudeseiteiten unter einem Winkel von 30° sieht.

Die roten Pfeile oben zeigen die Blickrichtung an. D.h, es wird von außen auf die Seiten des Gebäudes gesehen.Bedenke bitte, dass keine Kreise sondern (Fasskreis-)bögen konstruiert werden. Diese Bögen sind die möglichen Orte für die Blickposition $P$. Also müssen die Bögen auch außen liegen.

Ich erwähnte schon in diesem Kommentar, dass man den Winkel immer auf der gegenüberliegenden Seite der Strecke angelegt werden. Folglich ist eindeutig wo sie hier liegem - nämlich innen!

und wenn die Winkel innen liegen, so liegen die Fasskreisbögen außen. Und dann gibt es genau einen Schnittpunkt $P$.

Kommentiert 24 Mär 2022 von Werner-Salomon

ich denk eich weiss das schon,

hier Beispiel der große Kreis , habe ich einmal den Winkle innen(kommt rasu Kreis orange) und einmal außen ( komtmt rasu Kreis brauen) . Also der Fassungskreise kommt einmal außen und einmal innen aber die Lösung geht IMMER .also stimmt. wenn ich aber bei der kleinen Kreis so mach geht nicht? du siehst unten den Winkel 30 ( habe gelöscht) für den grossen Kries habe ich einmal innen und hat geklappt mit dem kleinen Kreis und gibt es einen Schnittpunkt ,und wenn ich den Winkel außer trage klappt imme Noch mit dem kleinen Kreis.

Aber

wenn ich den Winkel des kleinen Kreises ändere( ich trage den Winkel von aussen ) dann habe ich diese baluer Kreis ,dann klappt nicht mit den andere grossen Kreisen .

warum? Hast du mich verstanden

Kommentiert 26 Mär 2022 von Zahri Ameer

Ich habe die Zeichnung vergessen hinzufügen: ich füge hier ein: und stelle meine Frage noch mal:

lesen meine Frage bitte und gucke meine Zeichnung unten.

hier Beispiel der große Kreis , habe ich einmal den Winkle innen(kommt rasu Kreis orange) und einmal außen ( komtmt rasu Kreis brauen) . Also der Fassungskreise kommt einmal außen und einmal innen aber die Lösung geht IMMER .also stimmt. wenn ich aber bei der kleinen Kreis so mach geht nicht? du siehst unten den Winkel 30 ( habe gelöscht) für den grossen Kries habe ich einmal innen und hat geklappt mit dem kleinen Kreis und gibt es einen Schnittpunkt ,und wenn ich den Winkel außer trage klappt imme Noch mit dem kleinen Kreis.

Aber

wenn ich den Winkel des kleinen Kreises ändere( ich trage den Winkel von aussen ) dann habe ich diese baluer Kreis ,dann klappt nicht mit den andere grossen Kreisen .

warum? Hast du mich verstanden

Kommentiert 27 Mär 2022 von Zahri Ameer

Ein anderes Problem?

Stell deine Frage

oswald · Answer 1 · 2022-03-18T09:30:28+0000

Kann ich sagen: weil 2 * 3 sind BEIDE Primzahlen deswegen kommt 6 und dann 1260 durch 6 teilbar

Das ist richtig.

2 * 4 → Hier 4 ist KEINE prima deswegen kommt raus → 8 und dann geht nicht 1260 NICHT druch 8 teilbar ?

Das Problem ist nicht, das 4 keine Primzahl ist.

Das Problem ist, dass 2 und 4 nicht teilerfremd sind.

Beispiel.

Eine Zahl ist durch 210 teilbar, wenn sie durch 14 und durch 15 teilbar ist. Grund ist
- 14 · 15 = 210 und
- 14 und 15 sind teilerfremd.
Die Zahl 120 ist durch 8 teilbar und durch 10 teilbar, aber nicht durch 8 · 10 = 80 teilbar. Grund ist, dass 8 durch 2 teilbar ist und 10 durch 2 teilbar ist.

Allgemein gilt: Wenn eine Zahl durch $a$ teilbar ist und durch $b$ teilbar ist, dann ist sie auch durch $\operatorname{kgV}(a,b)$ teilbar.

Die Logik dahinter wird vielleicht klar, wenn man sich die Primfaktorzerlegung anschaut:

$\begin{aligned}\frac{1890}{210}&=\frac{1890}{14\cdot 15}=\frac{2\cdot 3^3\cdot 5\cdot 7}{(2\cdot 7)\cdot (3\cdot 5)}&&\text{hier kann gekürzt werden bis der Nenner 1 ist}\\\frac{120}{80}&=\frac{120}{8\cdot 10} = \frac{2^3\cdot 3\cdot 5}{(2^3)\cdot (2\cdot 5)}&&\text{hier bleibt im Nenner eine 2 übrig}\end{aligned}$

aber warum wenn ich in eine Kombination von 2 * 4 = 8 nehme, geht aber nicht 1260 ist NICHT durch 8 teilbar?

3 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: