Zeigen Sie:A->B.... injektiv surjektiv bijektiv

Question

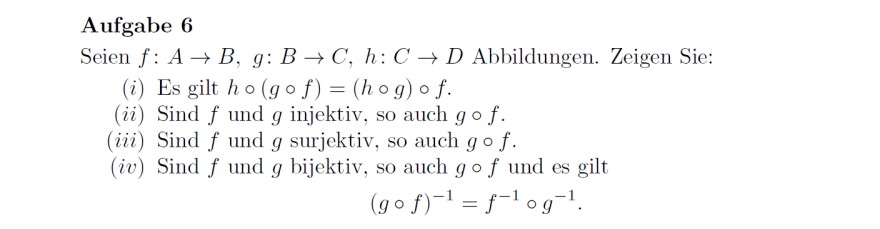
Text erkannt:

Aufgabe 6
Seien \( f: A \rightarrow B, g: B \rightarrow C, h: C \rightarrow D \) Abbildungen. Zeigen Sie:
(i) Es gilt \( h \circ(g \circ f)=(h \circ g) \circ f \).
(ii) Sind \( f \) und \( g \) injektiv, so auch \( g \circ f \).
(iii) Sind \( f \) und \( g \) surjektiv, so auch \( g \circ f \).
\( (i v) \) Sind \( f \) und \( g \) bijektiv, so auch \( g \circ f \) und es gilt
\( (g \circ f)^{-1}=f^{-1} \circ g^{-1} . \)

Aufgabe:

Aufgabe ist im Bild beschrieben

Problem/Ansatz:

Kann mir wer bitte sagen was die Punkte darstellen und hoch -1, bin auch leider schon beim verstehen der angabe etwas verloren vielleicht kanns wer anhand der Beispiele oben erklären.

Comments

hoch -1 Das bezeichnet die Umkehrabbildung einer

bijektiven Abbildung.

Answer 1

a) Für alle x∈A gilt  (ho(gof))(x) = h((gof)(x)) = h( g(f(x)) ) = (hog)(f(x))=((hog)of)(x).

Also \( h \circ(g \circ f)=(h \circ g) \circ f \)